【题目】在平面直角坐标系中,点A、B的坐标分别为(﹣3,0)、(3,0),点P在反比例函数y= ![]() 的图象上.若△PAB为直角三角形,则满足条件的点P的个数为( )
的图象上.若△PAB为直角三角形,则满足条件的点P的个数为( )
A. 2个 B. 4个 C. 5个 D. 6个
参考答案:
【答案】A
【解析】
设点P的坐标为(x,y),分∠APB=90°、∠PAB=90°和∠PBA=90°三种情况考虑:当∠APB=90°时,以AB为直径作圆,由圆与双曲线无交点可知此时点P不存在;当∠PAB=90°时,可找出x=-3,进而可得出点P的坐标;当∠PBA=90°时,可找出x=3,进而可得出点P的坐标.综上即可得出结论.
设点P的坐标为(x,y),
当∠APB=90°时,以AB为直径作圆,如图所示,
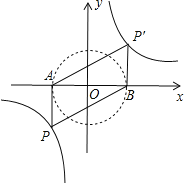
∵圆与双曲线无交点,
∴点P不存在;
当∠PAB=90°时,x=-3,
y=![]() =-3,
=-3,
∴点P的坐标(-3,-3),
当∠PBA=90°时,x=3,
y=![]() =3,
=3,
∴点P的坐标为(3,3).
综上所述:满足条件的点P有2个.
故选:A.
-
科目: 来源: 题型:
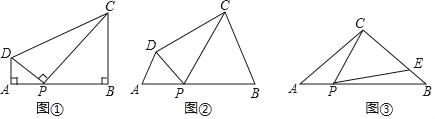
查看答案和解析>>【题目】(感知)如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC=90°.易证:△DAP∽△PBC(不要求证明).
(探究)如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC.
(1)求证:△DAP~△PBC.
(2)若PD=5,PC=10,BC=9,求AP的长.
(应用)如图③,在△ABC中,AC=BC=4,AB=6,点P在边AB上(点P不与点A、B重合),连结CP,作∠CPE=∠A,PE与边BC交于点E.当CE=3EB时,求AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线
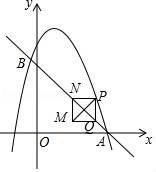 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为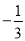 .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.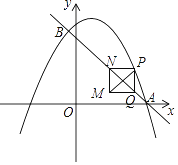
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B是反比例函数y=
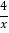 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )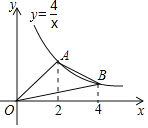
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P的坐标为(0,﹣5),以P为圆心的圆与x轴相切,⊙P的弦AB(B点在A点右侧)垂直于y轴,且AB=8,反比例函数
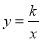 (k≠0)经过点B,则k=______.
(k≠0)经过点B,则k=______. -
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是( )
①甲骑车速度为30km/小时,乙的速度为20km/小时;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④
 小时后两人相遇.
小时后两人相遇.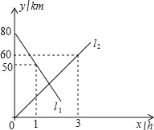
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数
 (x<0)图象上一点,AO的延长线交函数
(x<0)图象上一点,AO的延长线交函数 (x>0,k<0)的
(x>0,k<0)的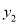 图象于点B,BC⊥x轴,若S△ABC=
图象于点B,BC⊥x轴,若S△ABC=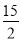 ,求函数y2的解析式.
,求函数y2的解析式.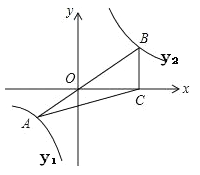
相关试题

