【题目】已知:将矩形纸片ABCD折叠,使点A与点C重合(点D与D'为对应点),折痕为EF,连接AF.
(1)如图1,求证:四边形AECF为菱形;
(2)如图2,若FC=2DF,连接AC交EF于点O,连接DO、D'O,在不添加任何辅助线的情况下,请直接写出图2中所有等边三角形.
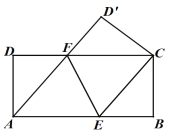

(图1) (图2)
参考答案:
【答案】(1)见解析(2)△AOD,△AEF,△CEF,△COD、
【解析】(1)先证明四边形AECF是平行四边形,再根据AE=CE,即可证明四边形AECF是菱形;
(2)根据等边三角形的判定方法可判定出等边三角形有△AEF、△CEF、△AOD、△COD′.
(1)∵将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,
∴AE=CE,AF=FC,∠AEF=∠CEF,
∵四边形ABCD是矩形,
∴∠ADC=∠BAD=90°,AE∥CF,
∴∠CFE=∠AEF,
∴∠CEF=∠CFE,
∴CF=CE,
∴AE=CF,
∴四边形AECF是平行四边形,
又∵AE=CE,
∴四边形AECF是菱形;
(2) 等边三角形为:△AEF、△CEF、△AOD、△COD′;理由如下:
∵FC=2DF,AF=FC,
∴AF=2DF,
∵∠ADC=90°,
∴∠DAF=30°,
∴∠EAF=60°,
∵四边形AECF是菱形,
∴AE=AF,△AEF≌△CEF,OA=OC=![]() AC,
AC,
∴△AEF和△CEF是等边三角形;
∵∠ADC=90°,
∴OD=![]() AC=OA,
AC=OA,
∵∠OAF=![]() ∠EAF=30°,
∠EAF=30°,
∴∠OAD=60°,
∴△AOD是等边三角形;
∵CD′=AD=OC,OD′=![]() AC,
AC,
∴CD′=OC=OD′,
∴△COD′是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产的
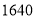 件新产品,需要精加工后才能投放市场.现把精加工新产品的任务分给甲、乙两人,甲加工新产品的数量要比乙多
件新产品,需要精加工后才能投放市场.现把精加工新产品的任务分给甲、乙两人,甲加工新产品的数量要比乙多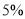 .
.(1)求甲、乙两人各需加工多少件新产品;
(2)已知乙比甲平均每天少加工
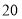 件新产品,用时比甲多用
件新产品,用时比甲多用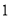 天时间.求甲平均每天加工多少件新产品.
天时间.求甲平均每天加工多少件新产品. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
(1)求a的值.
(2)求a名学生中选择去植物园春游的人数占所抽取人数的百分比是多少?
(3)如果该校八年级有440名学生,请你估计选择去太阳岛春游的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=BC,E是BC边上的一点,连接AE,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:△ACE≌△CBD;
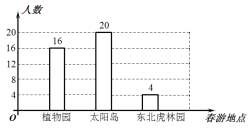
(2)若BE=3
 ,AB=6
,AB=6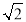 ,求点E到AB的距离.
,求点E到AB的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降,今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为90万元,今年销售额只有80万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知B款汽车每辆进价为7.5万元,每辆售价为10.5万元,A款汽车每辆进价为6万元,若卖出这两款汽车15辆后获利不低于38万元,问B款汽车至少卖出多少辆?
-
科目: 来源: 题型:
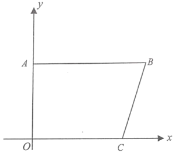
查看答案和解析>>【题目】如图,在平面直角坐标系
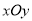 中,已知点
中,已知点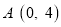 ,点
,点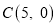 ,点
,点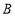 在第一象限内,
在第一象限内,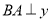 轴,且
轴,且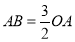 .
.
(1)求直线
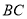 的表达式;
的表达式;(2)如果四边形
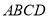 是等腰梯形,求点
是等腰梯形,求点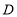 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某运输公司派出大小两种型号共20辆渣土运输车运输士方.已知一辆大型渣土运输车和两辆小型渣土运输车每次共运20吨;3辆大型渣土运输车和8辆小型渣土运输车每次共运70吨.并且一辆大型渣土运输车运输花费500元/次,一辆小型渣土运输车运输花费300元/次.
(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?
(2)若每次运输主方总不小于148吨,且小型渣土运输车至少派出7辆,问该渣土运输公司有哪几种派出方案?最少需要花费多少元?
相关试题

