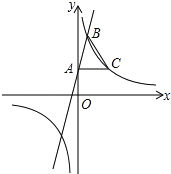
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+1的图象与y轴交于点A,与反比例函数y=![]() 在第一象限内的图象交于点B,且点B的横坐标为1,过点A作AC⊥y轴交反比例函数y=
在第一象限内的图象交于点B,且点B的横坐标为1,过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
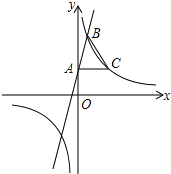
(1)求反比例函数的表达式及△ABC的面积;
(2)直接写出当x<1时,y=![]() (k≠0)中y的取值范围.
(k≠0)中y的取值范围.
参考答案:
【答案】(1)y=![]() ,S△ABC=
,S△ABC=![]() ACBD=
ACBD=![]() ×4×3=6;(2)当x<0时,y<0.
×4×3=6;(2)当x<0时,y<0.
【解析】
试题分析:(1)先由一次函数y=3x+1的图象过点B,且点B的横坐标为1,将x=1代入y=3x+1,求出y的值,得到点B的坐标,再将B点坐标代入y=![]() ,利用待定系数法即可求出反比例函数的表达式;根据一次函数y=3x+1的图象与y轴交于点A,求出点A的坐标为(0,1),再将y=1代入y=
,利用待定系数法即可求出反比例函数的表达式;根据一次函数y=3x+1的图象与y轴交于点A,求出点A的坐标为(0,1),再将y=1代入y=![]() ,求出x的值,那么AC=4.过B作BD⊥AC于D,则BD=yB﹣yC=4﹣1=3,然后根据S△ABC=
,求出x的值,那么AC=4.过B作BD⊥AC于D,则BD=yB﹣yC=4﹣1=3,然后根据S△ABC=![]() ACBD,将数值代入计算即可求解;
ACBD,将数值代入计算即可求解;
(2)根据x<1时,得到![]() ,于是得到y的取值范围.
,于是得到y的取值范围.
解:(1)∵一次函数y=3x+1的图象过点B,且点B的横坐标为1,
∴y=3×1+1=4,
∴点B的坐标为(1,4).
∵点B在反比例函数y=![]() 的图象上,
的图象上,
∴k=1×4=4,
∴反比例函数的表达式为y=![]() ,
,
∵一次函数y=3x+1的图象与y轴交于点A,
∴当x=0时,y=1,
∴点A的坐标为(0,1),
∵AC⊥y轴,
∴点C的纵坐标与点A的纵坐标相同,是1,
∵点C在反比例函数y=![]() 的图象上,
的图象上,
∴当y=1时,1=![]() ,解得x=4,
,解得x=4,
∴AC=4.
过B作BD⊥AC于D,则BD=yB﹣yC=4﹣1=3,
∴S△ABC=![]() ACBD=
ACBD=![]() ×4×3=6;
×4×3=6;
(2)由图形得:∵当0<x<1时,![]() ,
,
∴y>4,
当x<0时,y<0.
-
科目: 来源: 题型:
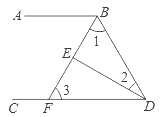
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于点E,BE的延长线交CD于点F,且∠1+∠2=90°.猜想∠2与∠3的关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有客房200间供游客居住,当每间客房的定价为每天180元时,客房恰好全部住满;如果每间客房每天的定价每增加10元,就会减少4间客房出租.设每间客房每天的定价增加
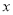 元,宾馆出租的客房为
元,宾馆出租的客房为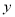 间.求:
间.求:(1)
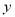 关于
关于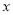 的函数关系式;
的函数关系式;(2)如果某天宾馆客房收入38400元,那么这天每间客房的价格是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个等边三角形木框,甲虫P在边框AC上爬行(A,C端点除外),设甲虫P到另外两边的距离之和为d,等边三角形ABC的高为h,则d与h的大小关系是( )
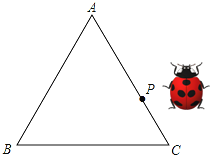
A.d>h B.d<h C.d=h D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接圆内两条相交直径的4个端点,围成的四边形一定是( ).
A.梯形 B.菱形 C.矩形 D.正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为( )
A. 2 cm B. 4 cm C. 6 cm D. 8 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是四边形ABCD的边AB上一点.
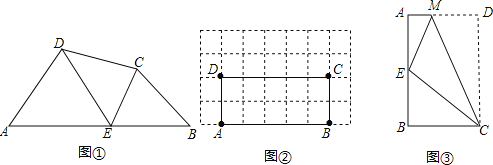
(1)猜想论证:如图,分别连接DE、CE,若∠A=∠B=∠DEC=65°,试猜想图中哪两个三角形相似,并说明理由.
(2)观察作图:如图,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图中矩形ABCD的边AB上画出所有满足条件的点E(点E与点A,B 不重合),分别连结ED,EC,使四边形ABCD被分成的三个三角形相似(不证明).
(3)拓展探究:如图,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好将四边形ABCM分成的三个三角形相似,请直接写出
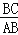 的值.
的值.
相关试题

