【题目】如图①,在平面直角坐标系中,直线y=﹣ ![]() x+
x+ ![]() 与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B.
与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B. 
(1)求⊙A的半径;
(2)连BF、AE,则BF与AE之间有什么位置关系?写出结论并证明.
(3)如图②,以AC为直径作⊙O1交y轴于M,N两点,点P是弧MC上任意一点,点Q是弧PM的中点,连CP,NQ,延长CP,NQ交于D点,求CD的长.
参考答案:
【答案】
(1)解:连接AF,如图①a.

∵直线y=﹣ ![]() x+
x+ ![]() 与x轴交于C点,与y轴交于E点,
与x轴交于C点,与y轴交于E点,
∴点C的坐标为(2,0),点E的坐标为(0, ![]() ),
),
∴OC=2,OE= ![]() .
.
∵∠EOC=90°,
∴EC= ![]() =
= ![]() .
.
∵AO⊥OE,∴直线OE与⊙A相切于点O.
又∵直线CE与⊙A相切于点F,
∴∠AFC=90°,EF=OE= ![]() ,
,
∴FC=FE+EC= ![]() +
+ ![]() =2
=2 ![]() .
.
在Rt△AFC中,
设AF=x,则AO=x,AC=x+2.
根据勾股定理可得:x2+(2 ![]() )2=(x+2)2,
)2=(x+2)2,
解得:x=1.
∴⊙A的半径为1
(2)解:BF∥AE.
证明:连接OF,交AE于点H,如图①b.

∵EF、EO分别与⊙A相切于点F、O,
∴EF=EO,EA平分∠FEO,
∴EA⊥OF,即∠AHO=90°.
∵BO是⊙A的直径,
∴∠BFO=90°,
∴∠BFO=∠AHO,
∴BF∥AE
(3)解:连接QC、QM、MC、NC、MO1,如图②.

∵AC是⊙O1的直径,AC⊥MN,
∴ ![]() ,
,
∴∠NQC=∠MNC.
∵∠MQC+∠MNC=180°,∠DQC+∠NQC=180°,
∴∠MQC=∠DQC.
∵点Q是 ![]() 的中点,
的中点,
∴∠MCQ=∠PCQ.
在△MCQ和△DCQ中,
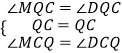 ,
,
∴△MCQ≌△DCQ(ASA),
∴MC=DC.
∵OA=1,OC=2,
∴AC=3,AO1= ![]() ,OO1=
,OO1= ![]() ,
,
在Rt△MOO1中,
MO1=AO1= ![]() ,OO1=
,OO1= ![]() ,
,
∴MO= ![]() =
= ![]() .
.
在Rt△MOC中,
MC= ![]() =
= ![]() ,
,
∴DC= ![]() .
.
∴CD的长为 ![]()
【解析】(1)连接AF,如图①a,由直线EC的解析式可求出OE、OC的长,根据勾股定理可求出EC的长,然后根据切线长定理可求出EF的长,然后在Rt△AFC中运用勾股定理就可求出圆的半径.(2)连接OF,交AE于点H,如图①b,根据切线长定理可得EF=EO,EA平分∠FEO,根据等腰三角形的性质可得∠AHO=90°,由BO是⊙A的直径可得∠BFO=90°,从而得到∠BFO=∠AHO,即可得到BF∥AE.(3)连接QC、QM、MC、NC、MO1 , 如图②,易证△MCQ≌△DCQ,则有MC=DC.在Rt△MOO1中,运用勾股定理可求出MO的长,然后在Rt△MOC中,运用勾股定理就可求出MC,即可得到CD的长.
【考点精析】解答此题的关键在于理解平行线的判定的相关知识,掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1 , 与x轴的另一个交点为A1 .

(1)当a=﹣1,b=1时,求抛物线n的解析式;
(2)四边形AC1A1C是什么特殊四边形,请写出结果并说明理由;
(3)若四边形AC1A1C为矩形,请求出a,b应满足的关系式. -
科目: 来源: 题型:
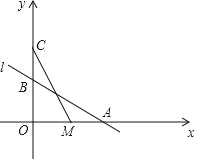
查看答案和解析>>【题目】如图,直线l:y=﹣
 x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.(1)求点A的坐标;
(2)请从A,B两题中任选一题作答.
A.求△COM的面积S与时间t之间的函数表达式;
B.当△ABM为等腰三角形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,点A,B,P,Q都在格点上.请按要求画出以AB为边的格点四边形.

(1)在图甲中画出一个ABCD,使得点P为ABCD的对称中心;
(2)在图乙中画出一个ABCD,使得点P,Q都在ABCD的对角线上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有2个,若从中随机摸出一个球,这个球是白球的概率为
 .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答) -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在公路上匀速行驶,下表记录的是汽车在加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时)
0
1
2
2.5
余油量y(升)
100
80
60
50
(1)小明分析上表中所给的数据发现x,y成一次函数关系,试求出它们之间的函数表达式(不要求写出自变量的取值范围);
(2)求汽车行驶4.2小时后,油箱内余油多少升?
相关试题

