【题目】在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色, ![]() 如此大量摸球实验后,小新发现其中摸出红球的频率稳定于
如此大量摸球实验后,小新发现其中摸出红球的频率稳定于![]() ,摸出黑球的频率稳定于
,摸出黑球的频率稳定于![]() ,对此实验,他总结出下列结论:
,对此实验,他总结出下列结论: ![]() 若进行大量摸球实验,摸出白球的频率稳定于
若进行大量摸球实验,摸出白球的频率稳定于![]() 若从布袋中任意摸出一个球,该球是黑球的概率最大;
若从布袋中任意摸出一个球,该球是黑球的概率最大; ![]() 若再摸球100次,必有20次摸出的是红球
若再摸球100次,必有20次摸出的是红球![]() 其中说法正确的是
其中说法正确的是![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】∵在一个不透明的布袋中,红球、黑球、白球共有若干个,其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%,
∴①若进行大量摸球实验,摸出白球的频率稳定于:1-20%-50%=30%,故此选项正确;
∵摸出黑球的频率稳定于50%,大于其它频率,
∴②从布袋中任意摸出一个球,该球是黑球的概率最大,故此选项正确;
③若再摸球100次,不一定有20次摸出的是红球,故此选项错误;
故正确的有①②.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 与
与 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与 轴交于点C,顶点为D,对称轴与
轴交于点C,顶点为D,对称轴与 轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交
轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交 轴交于点G.
轴交于点G.(1)如图①,求直线CE的解析式和顶点D的坐标;
(2)如图①,点P为直线CF上方抛物线上一点,连接PC、PF,当△PCF的面积最大时,点M是过P垂直于
 轴的直线l上一点,点N是抛物线对称轴上一点,求
轴的直线l上一点,点N是抛物线对称轴上一点,求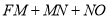 的最小值;
的最小值;(3)如图②,过点D作
 交
交 轴于点I,将△GDI沿射线GB方向平移至
轴于点I,将△GDI沿射线GB方向平移至 处,将
处,将 绕点
绕点 逆时针旋转
逆时针旋转 ,当旋转到一定度数时,点
,当旋转到一定度数时,点 会与点I重合,记旋转过程中的
会与点I重合,记旋转过程中的 为
为 ,若在整个旋转过程中,直线G’’I’’分别交x轴和直线GD’于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.
,若在整个旋转过程中,直线G’’I’’分别交x轴和直线GD’于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):
 .问:
.问:(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
-
科目: 来源: 题型:
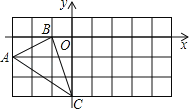
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,﹣1)、B(﹣1,0)、C(0,﹣3)
(1)点A关于坐标原点O对称的点的坐标为 .
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C,A1A的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向东走100米到聪聪家,再向西走150米到青青家,再向东走200米到刚刚家,请问:
【1】聪聪家与刚刚家相距多远?
【2】如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出他们家与学校的大概位置(数轴上50米表示单位1).
【3】聪聪家向西210米所表示的数是多少?
【4】你认为可用什么办法求数轴上两点之间的距离?
-
科目: 来源: 题型:
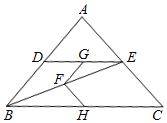
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是边AB的点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.
(1)求证:FG=FH;
(2)当∠A为多少度时,FG⊥FH?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-5)-(+3)+(-9)-(-7); (2)-|-2|-(-3)2÷(-1)2;
(3)
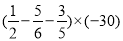 ; (4)-14-(1-0.5)÷
; (4)-14-(1-0.5)÷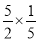 .
.
相关试题

