【题目】如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题。
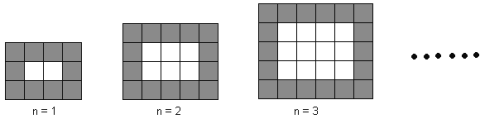
(1)在第4个图中,共有白色瓷砖 块;在第![]() 个图中,共有白色瓷砖 块;
个图中,共有白色瓷砖 块;
(2)在第4个图中,共有瓷砖 块;在第![]() 个图中,共有瓷砖 块;
个图中,共有瓷砖 块;
(3)如果每块黑瓷砖4元,白瓷砖3元,铺设当![]() 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖?
参考答案:
【答案】(1)20,n2+n;(2)42,(n+2)(n+3);(3)514元
【解析】
试题分析:(1)通过观察发现规律,然后将n=4代入即可;
(2)将黑色瓷砖和白色瓷砖加在一起即可得到答案;
(3)求出当n=10时黑色和白色瓷砖的个数,然后计算总费用即可.
(1)通过观察图形可知,当n=1时,用白瓷砖2块,黑瓷砖10块;
当n=2时,用白瓷砖6块,黑瓷砖14块;
当n=3时,用白瓷砖12块,黑瓷砖18块;
可以发现,需要白瓷砖的数量和图形数之间存在这样的关系,即白瓷砖块数等于图形数的平方加上图形数;
需要黑瓷砖的数量和图形数之间存在这样的关系,即黑瓷砖块数等于图形数的4倍加上图形数.
所以,在第n个图形中,白瓷砖的块数可用含n的代数式表示为![]() ;
;
黑瓷砖的块数可用含n的代数式表示为4n+6.
∴当n=4时,白色瓷砖有![]() 块;
块;
(2)由(1)可得总块数可表示为![]() ;
;
(3)观察图形可知,每-横行有白砖(n+1)块,每-竖列有白砖n块,
因而白砖总数是n(n+1)块,n=10时,白砖为10×11=110(块),黑砖数为46(块).
故总钱数为110×3+46×4=330+184=514(元),
答:共花514元钱购买瓷砖.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品进价为100元,标价为200元后再8折销售,则利润为( )
A. 50元 B. 60元 C. 70元 D. 80元
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和
(﹣2,0)之间,其部分图象如下图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填空:
(a-b)(a+b)=________;
(a-b)(a2+ab+b2)=________;
(a-b)(a3+a2b+ab2+b3)=________;
(2)猜想:
(a-b)(an-1+an-2b+an-3b2+…+abn-2+bn-1)=________(其中n为正整数,且n≥2);
(3)利用(2)猜想的结论计算:
①29+28+27+…+22+2+1;
②210-29+28-…-23+22-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
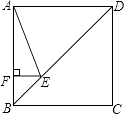
A.1
B.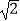
C.4﹣2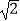
D.3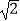 ﹣4
﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=
 AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( ) 
A.①②
B.②③
C.①③
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中∠C=90°,AC=BC=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为__.
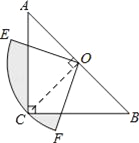
相关试题

