【题目】如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE,过点B作⊙O的切线交EC的延长线于点P.
(1)求证:AC2=AEAB;
(2)试判断PB与PE是否相等,并说明理由;
(3)设⊙O的半径为4,N为OC的中点,点Q在⊙O上,求线段PQ的最小值.

参考答案:
【答案】(1)(2)见解析;(3)线段PQ的最小值是![]() ﹣4.
﹣4.
【解析】分析:(1)证明△AEC∽△ACB,列比例式可得结论;
(2)如图2,证明∠PEB=∠COB=∠PBN,根据等角对等边可得:PB=PE;
(3)如图3,先确定线段PQ的最小值时Q的位置:因为OQ为半径,是定值4,则PQ+OQ的值最小时,PQ最小,当P、Q、O三点共线时,PQ最小,先求AE的长,从而得PB的长,最后利用勾股定理求OP的长,与半径的差就是PQ的最小值.
详解:证明:(1)如图1,连接BC,
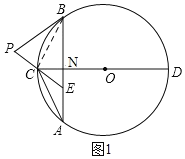
∵CD为⊙O的直径,AB⊥CD,
∴![]() =
=![]() ,
,
∴∠A=∠ABC,
∵EC=AE,
∴∠A=∠ACE,
∴∠ABC=∠ACE,
∵∠A=∠A,
∴△AEC∽△ACB,
∴![]()
∴![]()
(2)PB=PE,理由是:
如图2,连接OB,
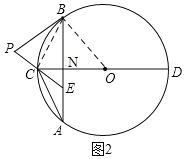
∵PB为⊙O的切线,
∴OB⊥PB,
∴![]()
∴![]()
∵![]()
∴∠PBN=∠COB,
∵∠PEB=∠A+∠ACE=2∠A,
∠COB=2∠A,
∴∠PEB=∠COB,
∴∠PEB=∠PBN,
∴PB=PE;
(3)如图3,∵N为OC的中点,
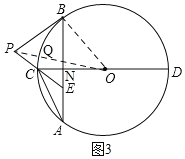
∴![]()
Rt△OBN中, ![]()
∴![]()
∵OC=OB,
∴△OCB为等边三角形,
∵Q为⊙O任意一点,
连接PQ、OQ,
因为OQ为半径,是定值4,
则PQ+OQ的值最小时,PQ最小,
当P、Q、O三点共线时,PQ最小,
∴Q为OP与⊙O的交点时,PQ最小,
![]()
∴![]()
![]()
∴△PBE是等边三角形,
Rt△OBN中, ![]()
∴![]()
设AE=x,则CE=x, ![]()
Rt△CNE中, ![]()
![]()
∴![]()
Rt△OPB中, ![]()
∴![]()
则线段PQ的最小值是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1 cm,△ACD的周长为12 cm,则△ABC的周长是( )

A. 13 cm B. 14 cm C. 15 cm D. 16 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
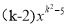 为反比例函数.
为反比例函数.(1)求k的值;
(2)它的图象在第 象限内,在各象限内,y随x增大而 ;(填变化情况)
(3)求出﹣2≤x≤﹣
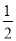 时,y的取值范围.
时,y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与反比例函数
的图象与反比例函数 的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).(1)利用图中条件,求反比例函数的解析式和m的值;
(2)求△DOC的面积.
(3)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
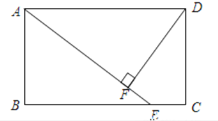
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )

A. 45°B. 60°C. 50°D. 55°
相关试题

