【题目】如图,ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延
长线分别交于点E、F.

(1)求证:△AOE≌△COF;
(2)请连接EC、AF,则EF与AC满足什么条件时,四边形AECF是矩形,并说明理由.
参考答案:
【答案】解:(1)证明:∵四边形ABCD是平行四边形,∴AO=OC,AB∥CD。
∴∠E=∠F又∠AOE=∠COF。∴△AOE≌△COF(ASA)。
(2)连接EC、AF,则EF与AC满足EF=AC时,四边形AECF是矩形。理由如下:

由(1)可知△AOE≌△COF,
∴OE=OF。
∵AO=CO,
∴四边形AECF是平行四边形。
∵EF=AC,
∴四边形AECF是矩形。
【解析】
试题分析:(1)根据平行四边形的性质和全等三角形的证明方法证明即可。
(2)连接EC、AF,则EF与AC满足EF=AC是,四边形AECF是矩形,首先证明四边形AECF是平行四边形,再根据对角线相等的平行四边形为矩形即可证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果水库的水位高于正常水位lm时,记作+1m,那么低于正常水位2m时,应记作 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的腰长是6,则底边长3,周长为______________________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:﹣2﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不论x取何值等式2ax+b=4x﹣3恒成立,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:﹣3x﹣(﹣x)= .
-
科目: 来源: 题型:
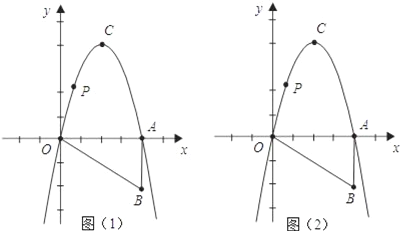
查看答案和解析>>【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.
相关试题

