【题目】如图,在△BCE中,点A时边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证明CB是⊙O的切线,只要证明BC⊥OB,可以证明△CDO≌△CBO解决问题.
(2)首先证明S阴=S扇形ODF,然后利用扇形面积公式计算即可.
试题解析:(1)证明:连接OD,与AF相交于点G,∵CE与⊙O相切于点D,∴OD⊥CE,∴∠CDO=90°,∵AD∥OC,∴∠ADO=∠1,∠DAO=∠2,∵OA=OD,∴∠ADO=∠DAO,∴∠1=∠2,在△CDO和△CBO中,∵CO=CO,∠1=∠2,OD=OC,∴△CDO≌△CBO,∴∠CBO=∠CDO=90°,∴CB是⊙O的切线.
(2)由(1)可知∠3=∠BCO,∠1=∠2,∵∠ECB=60°,∴∠3=![]() ∠ECB=30°,∴∠1=∠2=60°,∴∠4=60°,∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠1=∠ADO,在△ADG和△FOG中,∵∠1=∠ADG,∠FGO=∠AGD,AD=OF,∴△ADG≌△FOG,∴S△ADG=S△FOG,∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF=
∠ECB=30°,∴∠1=∠2=60°,∴∠4=60°,∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠1=∠ADO,在△ADG和△FOG中,∵∠1=∠ADG,∠FGO=∠AGD,AD=OF,∴△ADG≌△FOG,∴S△ADG=S△FOG,∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF=![]() =
=![]() .
.
-
科目: 来源: 题型:
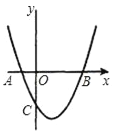
查看答案和解析>>【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于点C.
(1)点A的坐标为 ,点B的坐标为 ,点C的坐标为 .
(2)设抛物线y=x2﹣2x﹣3的顶点为M,求四边形ABMC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如表是某校合唱团成员的年龄分布统计,则这组数据(年龄)的中位数是( )
年龄
13
14
15
16
频数
5
7﹣a
13
a
A.13B.14C.15D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月28日全国部分宜居城市最高气温的数据如下:
宜居城市
大连
青岛
威海
金华
昆明
三亚
最高气温(℃)
25
28
35
30
26
32
则以上最高气温的中位数为℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(a4b)2÷a2的结果是( )
A.a2 b2
B.a6 b2
C.a7 b2
D.a8 b2 -
科目: 来源: 题型:
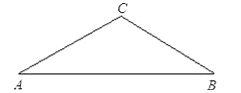
查看答案和解析>>【题目】如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,

(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,写出作法.
相关试题

