Question

【题目】如图（1），OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形．请你参考这个作全等三角形的方法，解答下列问题：

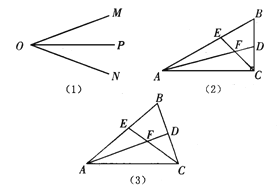
（1）如图（2），在△ABC中，∠ACB是直角，∠B＝60°， AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．请你判断并写出FE与FD之间的数量关系；

（2）如图（3），在△ABC中，如果∠ACB不是直角，而（1）中的其他条件不变，在（1）中所得结论是否仍然成立？请说明理由．

Answer 1

【答案】详见解析．

【解析】

试题分析：（1）在AC上截取AG=AE，连接FG．先证明△EAF≌△GAF，再证明△FDC≌△FGC，即可得结论；（2）根据（1）的方法证明即可．

试题解析：

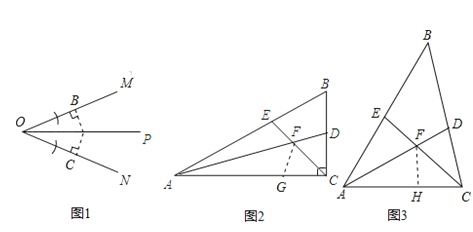
作对称全等三角形如图1．

（1）FE=FD．

如图2，∵∠ACB=90°，∠B=60°．

∴∠BAC=30°．

∵AD、CE分别是∠BAC和∠BCA的平分线，

∴∠EAF=∠CAF=∠BAC=15°，∠DCF=∠ACF=∠ACB=45°．

∴∠AEF=∠B+∠DCF=60°+45°=105°，

∴∠EFA=180°﹣∠AEF﹣∠EAF=60°．

如图2，在AC上截取AG=AE，连接FG．

∵∠EAF=∠GAF，

又∵AF为公共边，

∴△EAF≌△GAF，

∴FE=FG，∠EFA=∠GFA=60°．

∴∠GFC=180°﹣60°﹣60°=60°．

又∵∠DFC=∠EFA=60°，

∴∠DFC=∠GFC．

由（1）知∠DCF=∠GCF，

又∵CF为公共边，

∴△FDC≌△FGC，

∴FD=FG．

∴FE=FD．

（2）（1）中的结论FE=FD仍然成立．

同（2）可得△EAF≌△HAF，

∴FE=FH，∠EFA=∠HFA．

又由（1）知∠FAC=∠BAC，∠FCA=∠ACB，

∴∠FAC+∠FCA=（∠BAC+∠ACB）=（180°﹣∠B）=60°．

∴∠AFC=180°﹣（∠FAC+∠FCA）=120°．

∴∠EFA=∠HFA=180°﹣120°=60°．

同（2）可得△FDC≌△FHC，

∴FD=FH．

∴FE=FD．