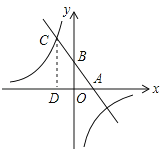
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;![]() 的解集.
的解集.

参考答案:
【答案】(1)y=﹣2x+6,![]() ;(2)(5,﹣4);(3)﹣2≤x<0或x≥5.
;(2)(5,﹣4);(3)﹣2≤x<0或x≥5.
【解析】
试题分析:(1)先求出A、B、C坐标,再利用待定系数法确定函数解析式.
(2)两个函数的解析式作为方程组,解方程组即可解决问题.
(3)根据图象一次函数的图象在反比例函数图象的下方,即可解决问题,注意等号.
试题解析:(1)∵OB=2OA=3OD=6,∴OB=6,OA=3,OD=2,∵CD⊥OA,∴DC∥OB,∴![]() ,∴
,∴![]() ,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴
,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴![]() 解得:
解得:![]() ,∴一次函数为y=﹣2x+6.
,∴一次函数为y=﹣2x+6.
∵反比例函数![]() 经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为
经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为![]() ;
;
(2)由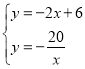 ,解得
,解得![]() 或
或![]() ,故另一个交点坐标为(5,﹣4);
,故另一个交点坐标为(5,﹣4);
(3)由图象可知![]() 的解集:﹣2≤x<0或x≥5.
的解集:﹣2≤x<0或x≥5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形两锐角;反之,两锐角互余的三角形是
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形两直角边的平方和等于;反之,有两边的平方和等于平方的三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
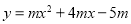 (m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线
(m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线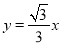 相交于点E,与x轴相交于点D,点P在直线
相交于点E,与x轴相交于点D,点P在直线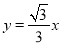 上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.(1)如图①所示,若抛物线顶点的纵坐标为
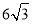 ,求抛物线的解析式;
,求抛物线的解析式;(2)求A、B两点的坐标;
(3)如图②所示,小红在探究点P的位置发现:当点P与点E重合时,∠PDF的大小为定值,进而猜想:对于直线
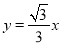 上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.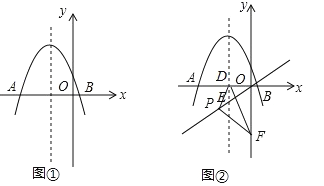
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中是必然事件的是( )
A.从一个装有黄、白两色球的缸里摸出一个球,摸出的球是白球;
B.小丹的自行车轮胎被钉子扎坏;
C.小红期末考试数学成绩一定得满分;
D.将豆油滴入水中,豆油会浮在水面上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P的坐标为(﹣2,a2+1),则点P所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】逆命题的定义:如果两个命题的题设和结论刚好相反,那么这样的两个命题叫做,如果把其中一个命题叫做原命题,那么另一个叫做它的
相关试题

