【题目】如图, ![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .以下四个结论:
.以下四个结论:
①![]() ;
;
②当![]() 为
为![]() 中点时
中点时![]() ;
;
③当![]() 时
时![]() ;
;
④当![]() 为等腰三角形时
为等腰三角形时![]() .
.
其中正确的结论是_________(把你认为正确结论的序号都填上)
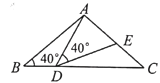
参考答案:
【答案】①②③
【解析】
利用三角形外角的性质可判断①;利用等腰三角形三线合一的性质得到∠ADC=90![]() ,求得∠EDC=50
,求得∠EDC=50![]() ,可判断②;利用三角形内角和定理求得∠DAC=70
,可判断②;利用三角形内角和定理求得∠DAC=70![]() =∠DEA,证得DA=DE,可证得
=∠DEA,证得DA=DE,可证得![]() ,可判断③;当
,可判断③;当![]() 为等腰三角形可分类讨论,可判断④.
为等腰三角形可分类讨论,可判断④.
①∠ADC是![]() 的一个外角,
的一个外角,
∴∠ADC =∠B+∠BAD=40![]() +∠BAD,
+∠BAD,
又∠ADC =40![]() +∠CDE,
+∠CDE,
∴∠CDE=∠BAD,故①正确;
②∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,AD⊥BC,
,AD⊥BC,
∴∠ADC=90![]() ,
,
∴∠EDC=90![]() ,
,
∴![]() ,
,
∴DE⊥AC,故②正确;
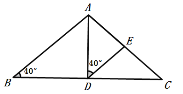
③当![]() 时
时
由①得∠CDE=∠BAD![]() ,
,
在![]() 中,∠DAC=
中,∠DAC=![]() ,
,
在![]() 中,∠AED=
中,∠AED=![]() ,
,
∴DA=ED,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,故③正确;
,故③正确;
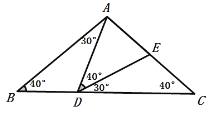
④当AD=AE时,∠AED=∠ADE=40°,
∴∠AED=∠C=40°,
则DE∥BC,不符合题意舍去;
当AD=ED时,∠DAE=∠DEA,
同③,![]() ;
;
当AE=DE时,∠DAE=∠ADE=40°,
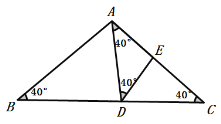
∴∠BAD![]() ,
,
∴当△ADE是等腰三角形时,
∴∠BAD的度数为30°或60°,故④错误;
综上,①②③正确,
故答案为:①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:
 ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈3.16)
≈3.16)
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师出示了如下的题目:如图1,在等边
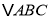 中,点
中,点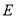 在
在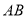 上,点
上,点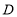 在
在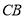 的延长线上,且
的延长线上,且 ,试确定线段
,试确定线段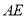 与
与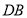 的大小关系,并说明理由,
的大小关系,并说明理由,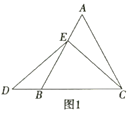
(1)小敏与同桌小聪探究解答的思路如下:
①特殊情况,探索结论,
当点
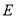 为
为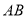 的中点时,如图2,确定线段
的中点时,如图2,确定线段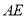 与
与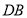 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论: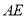 ______
______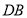 .(填>,<或=)
.(填>,<或=)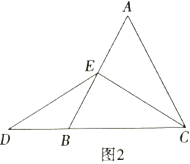
②特例启发,解答题目,
解:题目中,
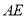 与
与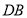 的大小关系是:
的大小关系是: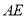 ______
______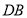 .(填>,<或=)
.(填>,<或=)理由如下:如图3,过点
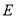 作
作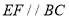 ,交
,交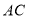 于点
于点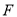 ,(请你补充完成解答过程)
,(请你补充完成解答过程)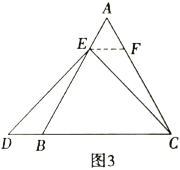
(2)拓展结论,设计新题,
同学小敏解答后,提出了新的问题:在等边
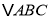 中,点
中,点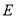 在直线
在直线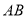 上,点
上,点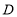 在直线
在直线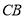 上,且
上,且 ,已知
,已知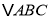 的边长为
的边长为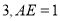 ,求
,求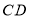 的长?(请直接写出结果)
的长?(请直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,则下列条件中不一定能使△ABC≌△ABD的是( )

A. AC=AD B. BC=BD C. ∠C=∠D D. ∠3=∠4
-
科目: 来源: 题型:
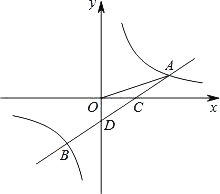
查看答案和解析>>【题目】如图,一次函数y=ax﹣1的图象与反比例函数y=
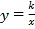 的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=
的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA= ,tan∠AOC=
,tan∠AOC= .
.(1)求a,k的值及点B的坐标;
(2)观察图象,请直接写出不等式ax﹣1≥
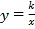 的解集;
的解集;(3)在y轴上存在一点P,使得△PDC与△ODC相似,请你求出P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)求购进甲、乙两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共80件,其中甲种纪念品的数量不少于60件.考虑到资金周转,用于购买这80件纪念品的资金不能超过7100元,那么该商店共有几种进货方案7
(3)若销售每件甲种纪含晶可获利润20元,每件乙种纪念品可获利润30元.在(2)中的各种进货方案中,若全部销售完,哪一种方案获利最大?最大利利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现
如图1,在Rt△ABC中,∠A=90°,
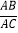 =1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.
=1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.(1)①求
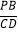 的值;②求∠ACD的度数.
的值;②求∠ACD的度数.(2)拓展探究
如图 2,在Rt△ABC中,∠A=90°,
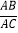 =k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.
=k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.(3)解决问题
如图 3,在△ABC中,∠B=45°,AB=4
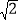 ,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.
,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.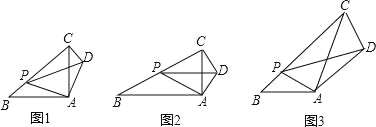
相关试题

