【题目】在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF. 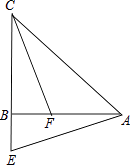
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=60°,求∠ACF的度数.
参考答案:
【答案】
(1)证明:在Rt△ABE和Rt△CBF中,
∵ ![]() ,
,
∴Rt△ABE≌Rt△CBF(HL)
(2)如图,∵在△ABC中,AB=CB,∠ABC=90°,
∴∠ACB=∠CAB=45°,
∴∠BAE=∠CAE﹣∠CAB=15°.
又由(1)知,Rt△ABE≌Rt△CBF,
∴∠BAE=∠BCF=15°,
∴∠ACF=∠ACB﹣∠BCF=30°.即∠ACF的度数是30°
【解析】(1)在Rt△ABE和Rt△CBF中,由于AB=CB,AE=CF,利用HL可证Rt△ABE≌Rt△CBF;(2)由等腰直角三角形的性质易求∠BAE=∠CAE﹣∠CAB=15°.利用(1)中全等三角形的对应角相等得到∠BAE=∠BCF=15°,则∠ACF=∠ACB﹣∠BCF=30°.即∠ACF的度数是30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
甲、乙两人同时从相距25千米的A地去B 地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在已知角内画射线,画1条射线,图中共有 个角;画2条射线,图中共有 个角;画3条射线,图中共有 个角;求画n条射线所得的角的个数 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
(1)求证:DQ=PQ;
(2)求AP·DQ的最大值;
(3)若P为AB的中点,求PG的长.
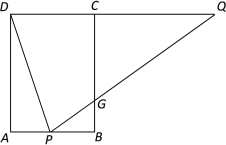
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角比它的余角的3倍大10°,则这个角等于________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请用学过的方法研究一类新函数
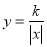 (k为常数,k≠0)的图象和性质.
(k为常数,k≠0)的图象和性质.(1)在给出的平面直角坐标系中画出函数
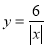 的图象(可以不列表);
的图象(可以不列表);(2)对于函数
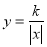 ,当自变量x的值增大时,函数值y怎样变化?
,当自变量x的值增大时,函数值y怎样变化?(3)函数
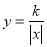 的图象可以经过怎样的变化得到函数
的图象可以经过怎样的变化得到函数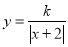 的图象?
的图象?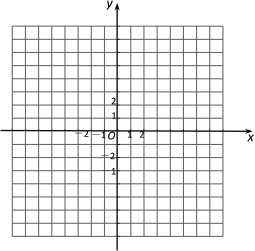
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于a的方程2(a+2)=a+4的解也是关于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使
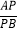 =b,点Q为PB的中点,请画出图形并求出线段AQ的长.
=b,点Q为PB的中点,请画出图形并求出线段AQ的长.
相关试题

