【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=_____°.

参考答案:
【答案】150°
【解析】
连结PQ,如图,根据等边三角形的性质得∠BAC=60°,AB=AC,再根据旋转的性质得AP=PQ=6,∠PAQ=60°,则可判断△APQ为等边三角形,所以PQ=AP=6,接着证明△APC≌△ABQ得到PC=QB=10,然后利用勾股定理的逆定理证明△PBQ为直角三角形,于是得到结论.
连结PQ,如图,
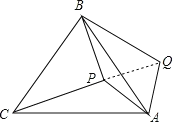
∵△ABC为等边三角形,
∴∠BAC=60![]() ,AB=AC,
,AB=AC,
∵线段AP绕点A顺时针旋转60![]() 得到线段AQ,
得到线段AQ,
∴AP=PQ=6,∠PAQ=60![]() ,
,
∴△APQ为等边三角形,
∴PQ=AP=6,
∵∠CAP+∠BAP=60![]() ,∠BAP+∠BAQ=60
,∠BAP+∠BAQ=60![]() ,
,
∴∠CAP=∠BAQ,
在△APC和△AQB中,
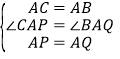 ,
,
∴△APC≌△AQB,
∴PC=QB=10,
在△BPQ中,
∵PB2=82=64,PQ2=62,BQ2=102,
而64+36=100,
∴PB2+PQ2=BQ2,
∴△PBQ为直角三角形,∠BPQ=90![]() ,
,
∴∠APB=90![]() +60
+60![]() =150
=150![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C处与地面的距离.(结果精确到0.1米,参考数据:
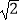 ≈1.41,
≈1.41, 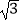 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读第(1)题,在解答过程后面空格中填写理由(依据),并解答第(2)题.
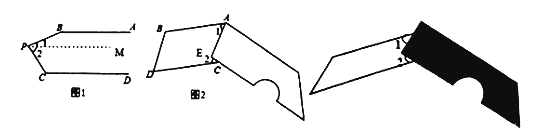
(1)已知,如图1:
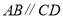 ,
,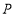 为
为 、
、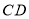 之间一点,求
之间一点,求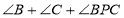 的大小.
的大小.解:过点
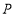 作
作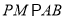 .
.∵
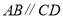 (已知).
(已知).∴
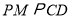 (_________________________),
(_________________________),∴
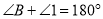 ,
,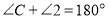 (_________________________).
(_________________________).∵
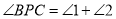 ,
,∴
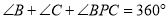 .
.
(2)如图,是我们生活中经常接触的小刀,刀片的外形如图2,刀片上、下是平行的,即
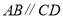 ,
,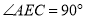 .转动刀片时会形成
.转动刀片时会形成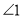 和
和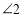 ,那么
,那么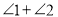 的大小是否会随刀片的转动面改变?说明理由.
的大小是否会随刀片的转动面改变?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在我校“书香校园”活动中,某数学小组为了解学生家庭藏书情况,随机抽取我校部分学生进行调查,并绘制成部分统计图如下表:
类别
家庭藏书情况统计表
学生人数
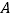

20
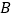
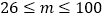
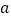

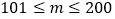
50
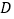
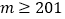
66
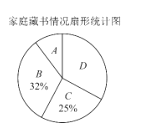
根据以上信息,解答下列问题:
(1)参加调查的学生人数为多少,a等于多少,本次调查结果的中位数在哪一类.
(2)在扇形统计图中,“
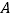 ”对应扇形的圆心角为多少.
”对应扇形的圆心角为多少.(3)若我校有4500名学生,请估计全校学生中藏书200本以上的人数.
-
科目: 来源: 题型:
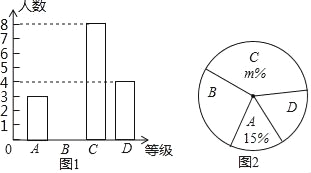
查看答案和解析>>【题目】为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成图1的条形统计图和图2扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)求参加比赛的学生共有多少名?并补全图1的条形统计图.
(2)在图2扇形统计图中,m的值为 ,表示“D等级”的扇形的圆心角为 度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
-
科目: 来源: 题型:
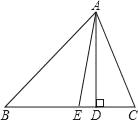
查看答案和解析>>【题目】如图,已知△ABC中,AD⊥BC于点D,AE为∠BAC的平分线,且∠B=36°,∠C=66°.求∠DAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.
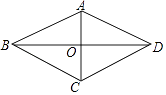
(1)求证:四边形ABCD是菱形;
(2)若CD=3,BD=2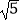 ,求四边形ABCD的面积.
,求四边形ABCD的面积.
相关试题

