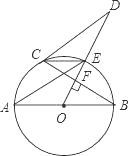
【题目】如图，AB是⊙O的直径，OD⊥弦BC于点F，交⊙O于点E，连结CE、AE、CD，若∠AEC=∠ODC．

（1）求证：直线CD为⊙O的切线；

（2）若AB=5，BC=4，求线段CD的长．

参考答案：

【答案】(1)证明见解析；（2）．

【解析】试题分析：（1）利用圆周角定理结合等腰三角形的性质得出∠OCF+∠DCB=90°，即可得出答案；

（2）利用圆周角定理得出∠ACB=90°，利用相似三角形的判定与性质得出DC的长．

试题解析：（1）连接OC，

∵∠CEA=∠CBA，∠AEC=∠ODC，

∴∠CBA=∠ODC，

又∵∠CFD=∠BFO，

∴∠DCB=∠BOF，

∵CO=BO，

∴∠OCF=∠B，

∵∠B+∠BOF=90°，

∴∠OCF+∠DCB=90°，

∴直线CD为⊙O的切线；

（2）连接AC，

∵AB是⊙O的直径，

∴∠ACB=90°，

∴∠DCO=∠ACB，

又∵∠D=∠B，

∴△OCD∽△ACB，

∵∠ACB=90°，AB=5，BC=4，

∴AC=3，

∴，即，

解得：DC=．

关闭