【题目】某快递公司快递员六月第三周投放快递物品件数为:有3天是20件,有1天是30件,有3天是40件,这周里日平均投递物品件数为( )
A.28件B.29件C.30件D.31件
参考答案:
【答案】C
【解析】
求出这7天的总件数,再求出平均数即可,也可以利用加权平均数的计算方法进行计算,即20件、30件、40件按3:1:3的比例进行计算.
解:(20×3+30+40×3)÷7=30件,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2+3a2=4a4B.a2b2b3=2a6b
C.(6a3b2)÷(3a)=2a2D.(﹣3a)2=9a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子正确的是( )
A.若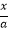 <
<  ,则x<y
,则x<y
B.若bx>by,则x>y
C.若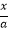 =
=  ,则x=y
,则x=y
D.若mx=my,则x=y -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2a2﹣4a+2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中的假命题是( )
A. 一组邻边相等的平行四边形是菱形
B. 一组邻边相等的矩形是正方形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边相等且有一个角是直角的四边形是矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学老师布置了这样一道作业题:
在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.
小聪提供了研究这个问题的过程和思路:先从特殊问题开始研究,当α=90°,β=30°时(如图1),利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形的相关知识便可解决这个问题.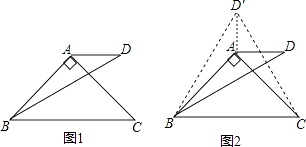
(1)请结合小聪研究问题的过程和思路,求出这种特殊情况下∠ADB的度数;
(2)结合小聪研究特殊问题的启发,请解决数学老师布置的这道作业题;
(3)解决完老师布置的这道作业题后,小聪进一步思考,当点D和点A在直线BC的异侧时,且∠ADB的度数与(1)中相同,则α,β满足的条件为(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是 .

相关试题

