【题目】如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
(1)△ABC的顶点都在方格纸的格点上,先将△ABC向右平移2个单位,再向上平移3个单位,得到△A1B1C1,其中点A1、B1、C1分别是A、B、C的对应点,试画出
△A1B1C1;
(2)连接AA1、BB1,则线段AA1、BB1的位置关系为 ,线段AA1、BB1的数量关系为 ;
(3)△A1B1C1的面积为 (平方单位)

参考答案:
【答案】(1)见解析 (2)平行,相等;(3)3.
【解析】
(1)按照题中要求将点A、B、C进行平移得到对应的点A1、B1、C1,再顺次连接A1、B1、C1三点即可得到所求△A1B1C1;
(2)如下图,连接AA1,BB1,再根据平移的性质进行解答即可;
(3)如下图所示,由图可知△A1B1C1中:A1C1=2,且A1C1边上的高为3,由此根据三角形的面积公式进行计算即可求得△A1B1C1的面积了.
(1)如图所示:△A1B1C1,即为所求;
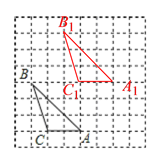
(2)如下图,连接AA1,BB1,
由平移的性质可得:线段AA1、BB1的位置关系为:平行;数量关系为:相等;
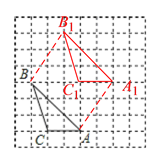
(3)由图可知:△A1B1C1中:A1C1=2,且A1C1边上的高为3,
∴△A1B1C1的面积为:![]() ×2×3=3.
×2×3=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个,摆放在迎宾大道两侧.已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆.
(l)某校2015届九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
-
科目: 来源: 题型:
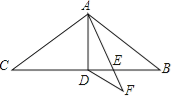
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.

(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(  ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 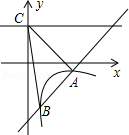
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
相关试题

