【题目】将一副三角板的直角重合放置,如图1所示,
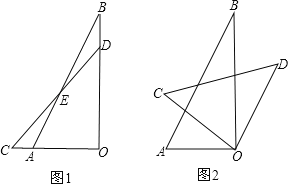
(1)图1中∠BEC的度数为_________
(2)三角板△AOB的位置保持不动,将三角板△COD绕其直角顶点O顺时针方向旋转:
①当旋转至图2所示位置时,恰好OD∥AB,求此时∠AOC的大小;
②若将三角板△COD继续绕O旋转,直至回到图1位置,在这一过程中,是否会存在△COD其中一边能与AB平行?如果存在,请你画出图形,并直接写出相应的∠AOC的大小;如果不存在,请说明理由.
参考答案:
【答案】(1)165°(2)①30°②120°存在
【解析】
试题分析:(1)由已知可求出∠CAE=180°﹣60°=120°,再根据三角形外角性质求出∠BEC的度数.
(2)①由OD∥AB可得∠BOD=∠B=30°,再由∠BOD+∠BOC=90°和∠AOC+∠BOC=90°求出∠AOC.
②将三角板△COD继续绕O旋转,OC边能与AB平行,由平行可得∠COB=∠B=30°,从而求出∠AOC.
解:(1)∠CAE=180°﹣∠BAO=180°﹣60°=120°,
∴∠BEC=∠C+∠CAE=45°+120°=165°,
故答案为:165°.
(2)①∵OD∥AB,
∴∠BOD=∠B=30°,
又∠BOD+∠BOC=90°,∠AOC+∠BOC=90°,
∴∠AOC=∠BOD=30°.

②存在,如图1,∠AOC=120°;
如图2,∠AOC=165°;
如图3,∠AOC=30°;
如图4,∠AOC=150°;
如图5,∠AOC=60°;
如图6,∠AOC=15°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班开展1分钟仰卧起坐比赛活动,5名同学的成绩如下(单位:个):37、38、40、40、42.这组数据的众数是( )
A. 37 B. 38 C. 40 D. 42
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学投掷实心球,每人投10次,平均成绩为18米,方差分别为S甲2=0.1,S乙2=0.04,成绩比较稳定的是__(填“甲”或“乙”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 相等的两个角是对顶角
B. 同位角相等
C. 图形平移后的大小可以发生改变
D. 两条直线相交所成的四个角都相等,则这两条直线互相垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐划一地排列在马路的一侧,AB、CD、EF是三个标杆,相邻的两个标杆之间的距离都是2 m,已知AB、CD在灯光下的影长分别为BM=1.6 m,DN=0.6m.
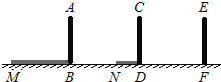
(1)请画出路灯O的位置和标杆EF在路灯灯光下的影子;
(2)求标杆EF的影长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,

(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.
-
科目: 来源: 题型:
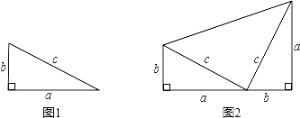
查看答案和解析>>【题目】勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你写出勾股定理内容(用文字语言表述):
[尝试证明]
以图1中的直角三角形为基础,可以构造出以a、b为底,以(a+b)为高的直角梯形(如图2),请你利用图2,证明勾股定理.
相关试题

