【题目】某校为了七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有学生中,每班随机抽取6名学生,并对他们的数学学习情况进行了问卷调查,我们从调查的题目中特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A—非常喜欢”、“B—比较喜欢”、“C—不太喜欢”、“D—很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项而且只能选一项)结果进行统计.现将统计结果制成如下两幅不完整的统计图.请你根据以上提供的信息,解答下列问题:
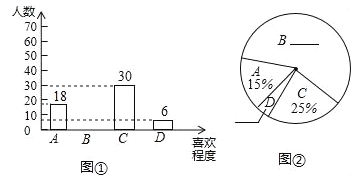
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取的学生对于数学学习喜欢程度的众数是:
(3)若该校七年级有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
参考答案:
【答案】(1)作图见解析;(2)比较喜欢(或填“B”);(3)240.
【解析】试题分析:(1)根据条形统计图与扇形统计图可以得到调查的学生数,从而可以的选B的学生数和选B和选D的学生所占的百分比,从而可以将统计图补充完整;
(2)根据(1)中补全的条形统计图可以得到众数;
(3)根据(1)中补全的扇形统计图可以得到该年级学生中对数学学习“不太喜欢”的人数.
试题解析:(1)由题意可得,调查的学生有:30÷25%=120(人),选B的学生有:120﹣18﹣30﹣6=66(人),B所占的百分比是:66÷120×100%=55%,D所占的百分比是:6÷120×100%=5%,故补全的条形统计图与扇形统计图如右图所示,(2)由(1)中补全的条形统计图可知,所抽取学生对数学学习喜欢程度的众数是:比较喜欢,故答案为:比较喜欢;
(3)由(1)中补全的扇形统计图可得,该年级学生中对数学学习“不太喜欢”的有:960×25%=240(人),即该年级学生中对数学学习“不太喜欢”的有240人.
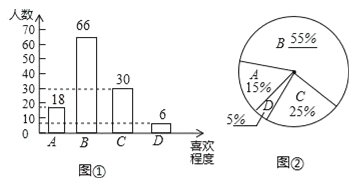
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a5(﹣a)3﹣a8的结果等于( )
A.0
B.﹣2a8
C.﹣a16
D.﹣2a16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC;
(2)若
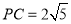 ,求⊙O的半径.
,求⊙O的半径.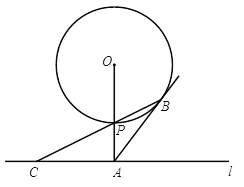
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“两直线平行,同位角相等”的逆命题是_____命题.(填“真”或“假”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫做分式不等式.如: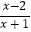 >0;
>0; 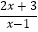 <0等.那么如何求出它们的解集呢?
<0等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若a>0,b>0,则 >0;若a<0,b<0,则
>0;若a<0,b<0,则  >0;解不等式
>0;解不等式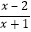 <0.
<0.
(2)若a>0,b<0,则 <0;若a<0,b>0,则
<0;若a<0,b>0,则  <0.
<0.
反之:①若 >0,则
>0,则 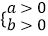 或
或 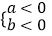 ,
,
②若 <0,则
<0,则 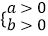 或
或 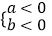 .
.
根据上述规律,①求不等式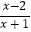 < 0的解集.
< 0的解集.
②直接写出不等式解集为x>3或x<1的最简分式不等式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量
房间价格
总维护费用
提价前
60
200
60×20
提价后
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
-
科目: 来源: 题型:
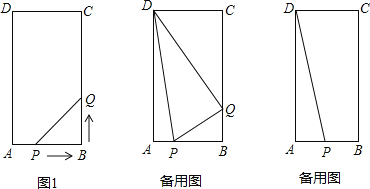
查看答案和解析>>【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)当运动开始后
 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;(3)在运动过程中,是否存在这样的时刻,使以Q为圆心,PQ为半径的圆正好经过点D?若存在,求出运动时间;若不存在,请说明理由.
相关试题

