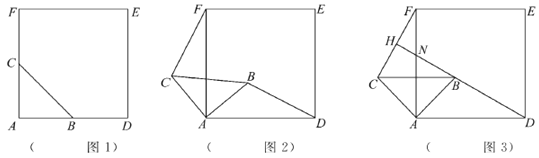
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3时,求线段DH的长.
参考答案:
【答案】(1)BD=CF成立,理由详见解析;(2)①详见解析;②.
【解析】
试题分析:(1)先用“SAS”证明△CAF≌△BAD,再用全等三角形的性质即可得BD=CF成立;(2)利用△HFN与△AND的内角和以及它们的等角,得到∠NHF=90°,即可得①的结论;(3)连接DF,延长AB,与DF交于点M,利用△BMD∽△FHD求解.
试题解析:(l)解:BD=CF成立.
证明:∵AC=AB,∠CAF=∠BAD=θ;AF=AD,△ABD≌△ACF,∴BD=CF.
(2)①证明:由(1)得,△ABD≌△ACF,∴∠HFN=∠ADN,
在△HFN与△ADN中,∵∠HFN=∠AND,∠HNF=∠AND,∴∠NHF=∠NAD=90°,
∴HD⊥HF,即BD⊥CF.
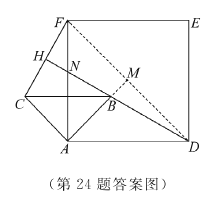
②解:如图,连接DF,延长AB,与DF交于点M.
在△MAD中,∵∠MAD=∠MDA=45°,∴∠BMD=90°.
在Rt△BMD与Rt△FHD中,∵∠MDB=∠HDF,∴△BMD∽△FHD.
∴AB=2,AD=3,四边形ADEF是正方形,∴MA=MD==3.
∴MB=3-2=1,DB==.
∵=.∴=.
∴DH=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级(1)班“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别为:4,6,8,16,16,这组数据的中位数、众数分别为( )
A.10,16B.16,16C.8,8D.8,16
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形的正投影不可能是( )
A.线段B.矩形C.正方形D.梯形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与关于直线
 成轴对称的△A′B′C′;
成轴对称的△A′B′C′;(2)线段CC′被直线
 ;
;(3)△ABC的面积为 ;
(4)在直线
 上找一点P,使PB+PC的长最短.
上找一点P,使PB+PC的长最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个书包的标价为115元,按8折出售仍可获利15%,该书包的进价为_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,错误的是( )
A.5a3﹣a3=4a3B.(﹣a)2a3=a5
C.(a﹣b)3(b﹣a)2=(a﹣b)5D.2m3n=6m+n
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE=
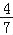 ,求
,求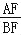 的值.
的值.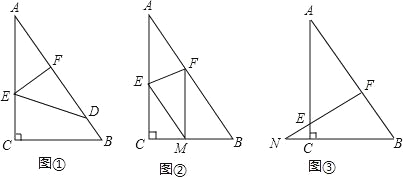
相关试题

