【题目】如图,正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,一次函数的图像经过点
,一次函数的图像经过点![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() .
.

(1)求一次函数的表达式;
(2)二元一次方程组![]() 的解为________________;
的解为________________;
(3)当![]() 与
与![]() 同时成立时,
同时成立时,![]() 的取值范围为__________;
的取值范围为__________;
(4)求![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)4
;(4)4
【解析】
(1)正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,已知正比例函数解析式可求得a,又因为一次函数的图像经过点
,已知正比例函数解析式可求得a,又因为一次函数的图像经过点![]() ,即可求出一次函数解析式.
,即可求出一次函数解析式.
(2)把两个一次函数解析式合成一个二元一次方程组,这个方程组的解就是它们的交点坐标.即可求解.
(3)分别求出![]() 与
与![]() 时x的取值范围,再取交集,即可求解.
时x的取值范围,再取交集,即可求解.
(4)(1)中已求得A点坐标,再求得OD长即可求出![]() 的面积.
的面积.
∵正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]()
![]()
∴![]()
又∵一次函数的图像经过点![]()
∴![]()
∴![]()
∴一次函数的表达式为:![]()
故答案为:![]()
(2)二元一次方程组![]() 的解即为正比例函数
的解即为正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交点坐标
的图像交点坐标
∵正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]()
∴二元一次方程组![]() 的解为:
的解为:![]()
故答案为:![]()
(3)当![]() 时
时
可得![]()
当![]() 时
时
∴![]()
∴![]()
∴当![]() 与
与![]() 同时成立时,
同时成立时,![]() 的取值范围为
的取值范围为![]()
故答案为:![]()
(3)令![]()
∴![]()
即OD=2
又∵![]()
S△AOD=![]() =4
=4
故答案为:4
-
科目: 来源: 题型:
查看答案和解析>>【题目】张华想用一块面积为400cm2的正方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2.他不知能否裁得出来,正在发愁.李明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意李明的说法吗?张华能用这块纸片裁出符合要求的纸片吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
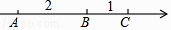
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着我国经济的高速发展,有着“经济晴雨表”之称的股市也得到迅速的发展,下表是今年上证指数某一周星期一至星期五的变化情况. (注:上周五收盘时上证指数为2616点,每一天收盘时指数与前一天相比,涨记为“+”,跌记为“-”)
星 期
一
二
三
四
五
指数的变化(与前一天比较)





⑴ 请求出这一周星期五收盘时的上证指数是多少点?
⑵ 说出这一周每一天收盘时上证指数哪一天最高?哪一天最低?分别是多少点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批节能灯,已知1只
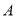 型节能灯和3只
型节能灯和3只 型节能灯共需11元;3只
型节能灯共需11元;3只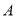 型节能灯和2只
型节能灯和2只 型节能灯共需12元.
型节能灯共需12元.(1)求一只
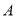 型节能灯和一只
型节能灯和一只 型节能灯的售价各是多少元?
型节能灯的售价各是多少元?(2)学校准备购进这两种型号的节能灯共30只,并且
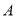 型节能灯的数量不多于
型节能灯的数量不多于 型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)11
 -1
-1 -1
-1 +4
+4 ;
;(2)(-22.84)-(+38.57)+(-37.16)-(-32.57);
(3)1
 -
- +2
+2 +
+ -4
-4 ;
;(4)(-36)-(-28)+(+125)+(-4)-(+53)-(-40).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
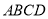 中,
中,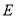 、
、 是对角线
是对角线 上的两点且
上的两点且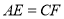 ,下列说法中正确的是( )
,下列说法中正确的是( )①
 ;②
;② ;③
;③ ;④四边形
;④四边形 为平行四边形;⑤
为平行四边形;⑤ ;⑥
;⑥ .
.
A.①⑥B.①②④⑥C.①②③④D.①②④⑤⑥
相关试题

