【题目】某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30
20 21 20 26 30 25 21 19 28 26
(1)请根据以上信息完成下表:
销售额(万元) | 17 | 19 | 20 | 21 | 25 | 26 | 28 | 30 |
频数(人数) | 1 | 1 | 3 | 3 |
(2)上述数据中,众数是 万元,中位数是 万元,平均数是 万元;
(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.
参考答案:
【答案】
【1】 3,5
【2】 26,25,24
【3】 不能
【解析】
解:(1)3,5……………………………1分
(2)26,25,24(每空1分)………4分
(3)不能………………………………5分
因为此时众数26万元![]() 中位数25万元…………………6分
中位数25万元…………………6分
(或:因为从统计表中可知20名营业员中,只有9名达到或超过目标,不到半数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
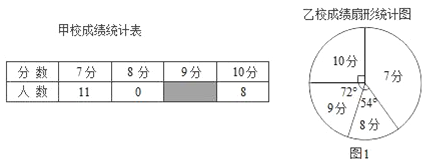
(1)在图1中,“7分”所在扇形的圆心角等于 °.
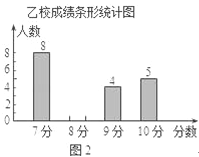
(2)请你将图2的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F.
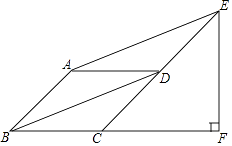
(1)求证:四边形ABCD是菱形;
(2)若∠ABC=45°,BC=2,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:
如图①,在△ABC中,点D、E、F分别在边AB、AC、CB上,且DE∥BC,EF∥AB,若∠ABC=65°,求∠DEF的度数.请将下面的解答过程补充完整,并填空(理由或数学式):

解:∵DE∥BC( )
∴∠DEF= ( )
∵EF∥AB
∴ =∠ABC( )
∴∠DEF=∠ABC( )
∵∠ABC=65°
∴∠DEF=
应用:
如图②,在△ABC中,点D、E、F分别在边AB、AC、BC的延长线上,且DE∥BC,EF∥AB,若∠ABC=β,则∠DEF的大小为 (用含β的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】汽车保有量是指一个地区拥有车辆的数量,一般是指在当地登记的车辆.进入21世纪以来,我国汽车保有量逐年增长.如图是根据中国产业信息网上的有关数据整理的统计图. 2007﹣2015年全国汽车保有量及增速统计图,

根据以上信息,回答下列问题:
(1)2016年汽车保有量净增2200万辆,为历史最高水平,2016年汽车的保有量为万辆,与2015年相比,2016年的增长率约为%;
(2)从2008年到2015年,年全国汽车保有量增速最快;
(3)预估2020年我国汽车保有量将达到万辆,预估理由是 .
相关试题

