【题目】边长为整数的直角三角形,若其两直角边边长是方程x2-(k+2)x+4k=0的两根,求k的值,并确定直角三角形三边之长。
参考答案:
【答案】解:设直角边为a,b(a<b),则a+b=k+2,ab=4k,因为方程的根为整数,故△=(k+2)2-16k为完全平方数。
设(k+2)2-16k=n2 ∴k2-12k+4=n2 ∴(k-6)2-n2=32
∴(k+n-6)(k-n-6)=1×32=2×16=4×8
∵k+n-6>k-n-6 ∴ ![]()
解得 ![]() ,k2=15,k3=12
,k2=15,k3=12
当k2=15时,a+b=17,ab=60 ∴a=15 , b=12 , c=13;当k=12时,a+b=14,ab=48
∴a=6 , b=8 ,c=10
【解析】根据方程的根为整数,得到根的判别式为平方数,然后进行讨论求出k值,得到三角形三边的长.根据直角三角形的直角边是整数,得到方程的根是整数,所以判别式是平方数,讨论求出k的值.然后求出直角三角形三边的长.
【考点精析】利用公式法和求根公式对题目进行判断即可得到答案,需要熟知要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= ( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=
 ( )
( )∠ABE=
 ( )
( )∴∠ADF=∠ABE
∴ ∥ ( )
∴∠FDE=∠DEB.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
 中,动点
中,动点 在
在 边上,以每秒
边上,以每秒 的速度从点
的速度从点 向点
向点 运动.
运动.(1)如图1,在运动过程中,若
 平分
平分 ,且满足
,且满足 ,求
,求 的度数.
的度数.(2)如图2,在(1)的条件下,连结
 并延长与
并延长与 的延长线交于点
的延长线交于点 ,连结
,连结 ,若
,若 ,求
,求 的面积.
的面积.(3)如图3,另一动点
 在
在 边上,以每秒
边上,以每秒 的速度从点
的速度从点 出发,在
出发,在 间往返运动,
间往返运动, 两点同时出发,当点
两点同时出发,当点 到达点
到达点 时停止运动(同时
时停止运动(同时 点也停止),若
点也停止),若 ,求当运动时间为多少秒时,以D,四点组成的四边形是平行四边形.
,求当运动时间为多少秒时,以D,四点组成的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
(1)写出点A、B的坐标:A(_____,_____)、B(_____,_____);
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,写出A′、B′、C′三点坐标;
(3)求△ABC的面积。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四个均由十六个小正方形组成的正方形网格中,各有一个三角形ABC,那么这四个三角形中,不是直角三角形的是( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等腰Rt△CEF的斜边CE在正方形ABCD的边BC的延长线上,CF>BC,取线段AE的中点M 。

(1)求证:MD=MF,MD⊥MF
(2)若Rt△CEF绕点C顺时针旋转任意角度(如图2),其他条件不变。(1)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,过对角线BD上点P作直线EF,GH分别平行于AB,BC,那么图中共有( )对面积相等平行四边形.
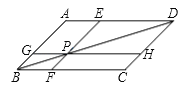
A. 1对B. 2对C. 3对D. 4对
相关试题

