【题目】如图,点E、A、C在一条直线上,给出下列三个事项:①AD⊥BC, EG⊥BC,垂足分别为D、G;②∠1=∠2;③AD平分∠BAC.

(1)以其中两个事项作为条件,另一个事项作为结论,你能组成 个正确的结论;
(2)请你选择其中一个正确结论进行说明理由.
解:以 为条件, 为结论.(填写序号)
理由是:
参考答案:
【答案】(1)2;(2)①②,③(或①③,②),证明见解析.
【解析】试题分析: (1)首先根据以其中两个事项作为条件,另一个事项作为结论有3种情况,再判断是否都正确,从而得到正确的个数.
(2)根据AD⊥BC, EG⊥BC得到AD∥EG,根据平行线的性质得到∠1=∠CAD, ∠2 =∠BAD,因为∠1=∠2 (或∠CAD=∠BAD),得到∠CAD=∠BAD (∠1=∠2).
试题解析:
(1)2
(2)①②,③(或①③,②)
∵AD⊥BC, EG⊥BC
∴∠ADC =∠EGC=90°
∴AD∥EG
∴∠1=∠CAD, ∠2=∠BAD
∵∠1=∠2 (或∠CAD=∠BAD)
∴∠CAD=∠BAD (∠1=∠2)
∴AD平分∠BAC
-
科目: 来源: 题型:
查看答案和解析>>【题目】李欣同学下午5:30放学离校,此刻时钟上时针与分针的夹角大小应为________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=
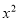 +bx+c经过A,B两点,抛物线的顶点为D.
+bx+c经过A,B两点,抛物线的顶点为D.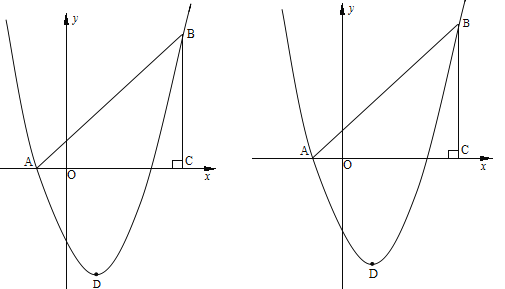
(1)、求b,c的值;
(2)、点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)、在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形? 若存在,求出所有点P的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出了点A、点B′、点C和它的对应点C′.

(1)请画出平移前后的△ABC和△A′B′C′;
(2)利用网格画出△ABC 中BC边上的中线AD;
(3)利用网格画出△ABC 中AB边上的高CE;
(4)△A′B′C′的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列等式:
(1)32﹣12=8,
(2)52﹣32=16,
(3)72﹣52=24,
……
(1)请仔细观察,写出第4个式子;
(2)根据以上式子的规律,写出第n个式子,并用所学知识说明第n个等式成立;
(3)利用(2)中发现的规律计算:8+16+24+…+792+800.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D落到D’处,折痕为EF.
(1)、求证:△ABE≌△AD’F;
(2)、连接CF,判断四边形AECF是否为平行四边形?请证明你的结论。
(3)、若AE=5,求四边形AECF的周长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】五边形的外角和等于度.
相关试题

