【题目】小聪和小慧去某风景区游览,两人在景点古刹处碰面,相约一起去游览景点飞瀑,小聪骑自行车先行出发,小慧乘电动车出发,途径草甸游玩后,再乘电动车去飞瀑,结果两人同时到达飞瀑.图中线段![]() 和折线
和折线![]() 表示小聪、小慧离古刹的路程
表示小聪、小慧离古刹的路程![]() (米)与小聪的骑行时间
(米)与小聪的骑行时间![]() (分)的函数关系的图象,根据图中所给信息,解答下列问题:
(分)的函数关系的图象,根据图中所给信息,解答下列问题:
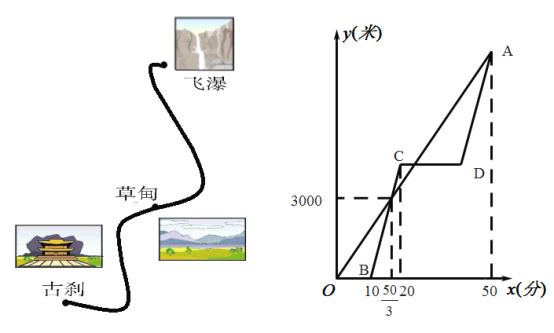
(1)小聪的速度是多少米/分?从古刹到飞瀑的路程是多少米?
(2)当小慧第一次与小聪相遇时,小慧离草甸还有多少米?
(3)在电动车行驶速度不变的条件下,求小慧在草甸游玩的时间.
参考答案:
【答案】(1)180,9000;(2)小慧与小聪第一次相遇时,离草甸还有1500米;(3)20分钟.
【解析】
(1)根据路程÷事件=速度,代入即可求出小聪的速度,再利用公式速度×时间求出路程即可.
(2)先利用待定系数法解出小慧的速度直线表达式,将x=20代入解出y的值与3000相减即可得到答案.
(3)用总时间减去到达草甸的时间和离开草甸到飞瀑的时间即可得到游玩时间.
(1)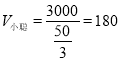 米/分.
米/分.
古刹到飞瀑的路程![]() 米
米
(2)设![]()
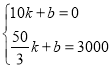 解得
解得![]()
![]()
当![]() ,
,![]()
![]() 米
米
答:小慧与小聪第一次相遇时,离草甸还有1500米。
(3)![]() 米
米
![]() .
.
![]()
答:20分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中正确的结论有( )
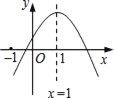
A. ①③ B. ②③ C. ①④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一块等腰直角三角板
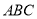 放置在平面直角坐标系中,
放置在平面直角坐标系中,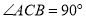 ,
,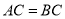 ,点
,点 在
在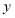 轴的正半轴上,点
轴的正半轴上,点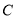 在
在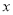 轴的负半轴上,点
轴的负半轴上,点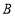 在第二象限,
在第二象限,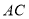 所在直线的函数表达式是
所在直线的函数表达式是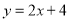 ,若保持
,若保持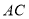 的长不变,当点
的长不变,当点 在
在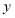 轴的正半轴滑动,点
轴的正半轴滑动,点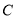 随之在
随之在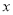 轴的负半轴上滑动,则在滑动过程中,点
轴的负半轴上滑动,则在滑动过程中,点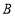 与原点
与原点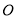 的最大距离是__________.
的最大距离是__________.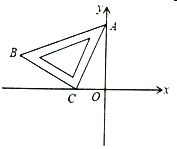
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
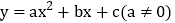 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为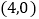 ,抛物线的对称轴是
,抛物线的对称轴是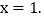 下列结论中:
下列结论中: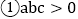 ;
;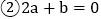 ;
; 方程
方程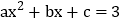 有两个不相等的实数根;
有两个不相等的实数根;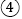 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为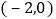 ;
; 若点
若点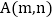 在该抛物线上,则
在该抛物线上,则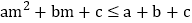 .
.其中正确的有
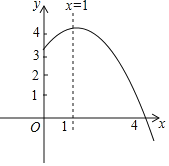
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),有下列结论:①2a+b=0,②abc>0;③方程ax2+bx+c=3有两个相等的实数根,④当y<0时,﹣2<x<4,其中正确的是( )
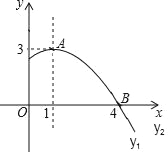
A. ②③ B. ①③ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
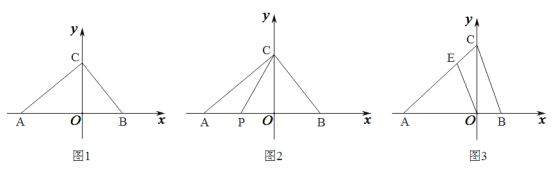
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
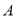 ,
,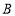 在
在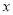 轴上,
轴上,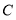 在
在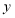 轴上,
轴上,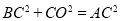 .
.
(1)求证:
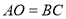 ;
;(2)如图2,若点
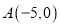 ,
,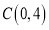 ,现有一个动点
,现有一个动点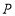 从点
从点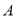 出发,沿着
出发,沿着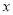 轴正方向运动,连结
轴正方向运动,连结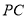 ,当
,当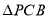 为等腰三角形时,求点
为等腰三角形时,求点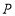 的坐标;
的坐标;(3)如图3,若
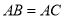 ,点
,点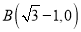 ,过
,过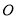 作
作 交
交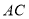 于
于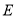 ,求
,求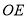 的长.
的长.
相关试题

