【题目】某校开展“爱我汕头,创文同行”的活动,倡议学生利用双休日参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:

(1)抽查的学生劳动时间为1.5小时”的人数为 人,并将条形统计图补充完整.
(2)抽查的学生劳动时间的众数为 小时,中位数为 小时.
(3)已知全校学生人数为1200人,请你估算该校学生参加义务劳动1小时的有多少人?
参考答案:
【答案】(1)40,补图见解析;(2)1.5、1.5;(3)估算该校学生参加义务劳动1小时的有400人.
【解析】
(1)根据统计图,先求出总数,再算出劳动时间为1.5小时的人数;(2)根据中位数和众数的定义分析即可;(3)用样本估计总体.
(1)40
(2)1.5,1.5
(3)1200×30%=400,
答:估算该校学生参加义务劳动1小时的有400人。
-
科目: 来源: 题型:
查看答案和解析>>【题目】张家界到长沙的距离约为320km,小明开着大货车,小华开着小轿车,都从张家界同时去长沙,已知小轿车的速度是大货车的1.25倍,小华比小明提前1小时到达长沙.试问:大货车和小轿车的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.

(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BE是线段AB的延长线,且∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断____∥_____,根据是_____________;
(2)由∠CBE=∠C可以判断____∥_____,根据是_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )

A.28°
B.33°
C.34°
D.56° -
科目: 来源: 题型:
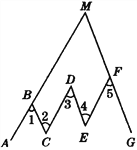
查看答案和解析>>【题目】如图,在折线ABCDEFG中,已知∠1=∠2=∠3=∠4=∠5,延长AB、GF交于点M.试探索∠AMG与∠3的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB,试说明:AF∥CE。

解:(1)因为∠DAB=∠DCB( ),
又AF平分∠DAB,
所以_____=
 ∠DAB( ),
∠DAB( ),又因为CE平分∠DCB,
所以∠FCE=_____( ),
所以∠FAE=∠FCE。
因为∠FCE=∠CEB,
所以______=________
所以AF∥CE( )
相关试题

