搜索
【题目】在平面直角坐标系中，把△ABC经过平移得到△A′B′C′，若A（1，m），B（4，2），点A的对应点A′（3，m+2），则点B对应点B′的标为（ ）
A. （6，5）B. （6，4）C. （5，m）D. （6，m）
参考答案：
【答案】B
【解析】
先根据点A与点A′的坐标确定平移规律，再根据规律写出点B的对应点B′的坐标即可．
解：∵把△ABC经过平移得到△A′B′C′，点A（1，m）的对应点为A′（3，m+2），
∴平移规律是：先向右平移2个单位，再向上平移2个单位，
∵点B的坐标为（4，2），
∴点B对应点B′的坐标为（6，4）．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列各式：
13+23=
×4×9= ×22×32
13+23+33=36= ×9×16= ×32×42
13+23+33+43=100= ×16×25= ×42×52
（1）计算：13+23+33+43+…+103的值；
（2）猜想：13+23+33+43+…+n3的值．
（3）计算：513+523+533+…+993+1003的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图1，菱形ABCD的边长为6，∠DAB=60°，点E是AB的中点，连接AC、EC．点Q从点A出发，沿折线A﹣D﹣C运动，同时点P从点A出发，沿射线AB运动，P、Q的速度均为每秒1个单位长度；以PQ为边在PQ的左侧作等边△PQF，△PQF与△AEC重叠部分的面积为S，当点Q运动到点C时P、Q同时停止运动，设运动的时间为t．
（1）当等边△PQF的边PQ恰好经过点D时，求运动时间t的值；当等边△PQF的边QF 恰好经过点E时，求运动时间t的值；
（2）在整个运动过程中，请求出S与t之间的函数关系式和相应的自变量t的取值范围；
（3）如图2，当点Q到达C点时，将等边△PQF绕点P旋转α°（0＜α＜360），直线PF分别与直线AC、直线CD交于点M、N．是否存在这样的α，使△CMN为等腰三角形？若存在，请直接写出此时线段CM的长度；若不存在，请说明理由．
-
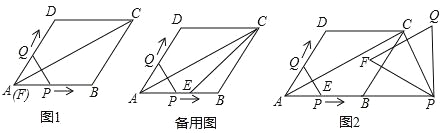
科目： 来源： 题型：
查看答案和解析>>【题目】一个三角形的两边分别是5cm和3cm，则第三边xcm的取值范围是_______________
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB=DC，AC=DB，AC与DB交于点M．过点C作CN∥BD，过点B作BN∥AC，CN与BN交于点N．
（1）求证：△ABC≌△DCB；
（2）求证：四边形BNCM是菱形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】以下表格是某校初一（1）班班长候选人得票数领先的三位同学的得票情况，则小明得票的频数是（ ）
候选人
小红
小明
小丽
唱票记录
正正正一
正
正正正正正一
A.16
B.5
C.21
D.42 -
科目： 来源： 题型：
查看答案和解析>>【题目】一个射手连续射靶10次，其中1次射中10环，6次射中9环，3次射中8环，则射中（ ）环的频数最大．
A.6
B.8
C.9
D.10
相关试题
