【题目】如图,AB是⊙O的直径, ![]() =
= ![]() ,且AB=5,BD=4,求弦DE的长.
,且AB=5,BD=4,求弦DE的长. 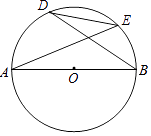
参考答案:
【答案】解:连接AD, ∵ ![]() =
= ![]() ,
,
∴AD=DE,
又∵AB为直径,
∴∠ADB=90°,
∵AB=5,BD=4,
∴DE=AD= ![]() =3,
=3,
∴DE的长为3.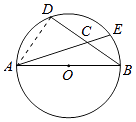
【解析】连接AD,在Rt△ABD中利用勾股定理求出AD,根据等弧对等弦得出AD=DE.
【考点精析】根据题目的已知条件,利用勾股定理的概念和圆心角、弧、弦的关系的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
(1)一个学生有中国邮票和外国邮票共25张,中国邮票的张数比外国邮票的张数的2倍少2张,这个学生有中国邮票和外国邮票各多少张?
(2)甲乙二人相距18千米,二人同时出发相向而行,1小时相遇;同时出发同向而行,甲3小时可以追上乙。求二人的平均速度各是多少?
(3)国家为九年义务教育期间的学生实行“两免一补”政策,下表是某地区某中学国家免费提供教科书补助的部分情况。
七
八
九
合计
每人免费补助金额(元)
110
90
50
——
人数(人)
80
300
免费补助金额(元)
4000
26200
请问该校七、八年级各有学生多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,直线
 相交于点
相交于点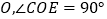 .
.(1)若
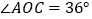 ,求
,求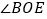 的度数;
的度数;(2)若
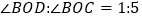 ,求
,求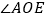 的度数;
的度数;(3)在(2)的条件下,过点
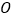 作
作 ,求
,求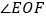 的度数.
的度数.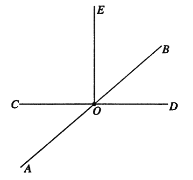
-
科目: 来源: 题型:
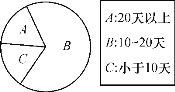
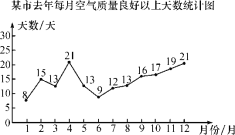
查看答案和解析>>【题目】空气质量状况已引起全社会的广泛关注,某市统计了去年每月空气质量达到良好以上的天数,整理后制成如图所示的折线统计图和扇形统计图.根据以上信息解答下列问题:该市去年空气质量连续提升的月份范围是____;扇形统计图中扇形A的圆心角的度数为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,我市城市居民用电收费方式有以下两种:
普通电价付费方式:全天0. 52元/度;
峰谷电价付费方式:峰时(早8:00~晚21:00)0. 65元/度;谷时(晚21:00~早8:00)0. 40元/度.
(1)小丽老师家10月份总用电量为280度.
①若其中峰时电量为80度,则小丽老师家按照哪种方式付电费比较合适?能省多少元?
②若小丽老师交费137元,那么,小丽老师家峰时电量为多少度?
(2)到11月份付费时,小丽老师发现11月份总用电量为320度,用峰谷电价付费方式比普通电价付费方式省了18. 4元,那么,11月份小丽老师家峰时电量为多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分) 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;
(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M点N的距离相等,则x= .
(2)数轴上是否存在点P,使点P到点M、点N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
(3)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.

相关试题

