【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
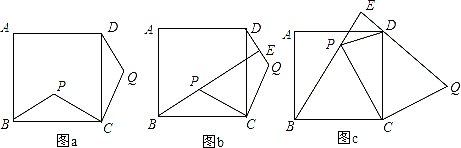
(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
参考答案:
【答案】(1)、证明过程见解析;(2)、①、证明过程见解析;②、等腰直角三角形,证明过程见解析.
【解析】
试题分析:(1)、根据正方形性质得出BC=DC,根据旋转图形的性质得出CP=CQ以及∠PCB=∠QCD,从而得出三角形全等;(2)、①、根据全等得出∠PBC=∠QBC,设BE和CD交点为M,根据对顶角得出∠DME=∠BMC,从而说明BE⊥QD;②、根据等边三角形的性质得出PB=PC=BC,∠PBC=∠BPC=∠PCB=60°,则∠PCD=30°,根据BC=DC,CP=CQ得出△PCD为等腰三角形,然后根据△DCQ为等边三角形,从而得出∠DEP=90°,从而得出答案.
试题解析:(1)、∵四边形ABCD是正方形,∴BC=DC
又∵将线段CP绕点C顺时针旋90°得到线段CQ,∴CP=CQ,∠PCQ=90°∴∠PCD+∠QCD=90°
又∵∠PCB+∠PCD=90° ∴∠PCB=∠QCD
在△BCP和△DCQ中 BC=DC,CP=CQ,∠PCB=∠QCD ∴△BCP≌△DCQ
(2)、①∵△BCP≌△DCQ ∴∠PBC=∠QBC
设BE和CD交点为M ∴∠DME=∠BMC ∠MED=∠MCB=90°∴BE⊥QD
②△DEP为等腰直角三角形,
∵△BOP为等边三角形 ∴PB=PC=BC ∠PBC=∠BPC=∠PCB=60°
∴∠PCD=90°-60°=30°∴∠DCQ=90°-60°=30°
又∵BC=DC CP=CQ∴PC=DC DC=CQ ∴△PCD是等腰三角形
△DCQ是等边三角形 ∴∠CPD=∠CDP=75°∠CDQ=60°∴∠EPD=180°-15°-60°=45°
∠EDP=180°-75°-60°=45 °∴∠EPD=∠EDP PE=DE ∴∠DEP=180°-45°-45°=90°
∴△DEP是等腰直角三形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌电插座抽样检查的合格率为99%,则下列说法总正确的是( )
A. 购买100个该品牌的电插座,一定有99个合格
B. 购买1000个该品牌的电插座,一定有10个不合格
C. 购买20个该品牌的电插座,一定都合格
D. 即使购买一个该品牌的电插座,也可能不合格
-
科目: 来源: 题型:
查看答案和解析>>【题目】“角平分线上的点到角两边的距离相等”的逆命题是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.
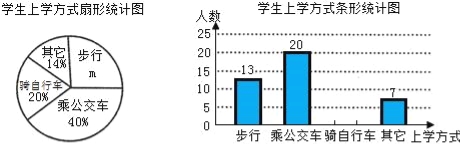
(1)m= %,这次共抽取 名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有1500名学生,请你估计该校骑自行车上学的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于有序数对的说法正确的是( )
A.(3,2)与(2,3)表示的位置相同
B.(a,b)与(b, a)表示的位置不同
C.(3,+2)与(+2,3)是表示不同位置的两个有序数对
D.(4, 4)与(4,4)表示两个不同的位置
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值.
a(a+2)-(a5+3a3)÷a3其中a=-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“平行四边形的两条对角线互相平分”的逆命题是_________命题(填“真”或“假”).
相关试题

