【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为70.
⑴请写出AB的中点M对应的数
![]()
⑵现在有一只电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2个单位/秒的速度向左运动,设两只电子蚂蚁在数轴上的C点相遇,请你求出C点对应的数 .
⑶若当电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2单位/秒的速度向左运动,经过多长时间两只电子蚂蚁在数轴上相距35个单位长度,并写出此时P点对应的数.
参考答案:
【答案】(1)30;(2)C点对应的数是38;(3)经过9秒或23秒,2只电子蚂蚁在数轴上相距35个单位长度,9秒对应的数为17,23秒对应的数为59.
【解析】试题
(1)由点A对应的数为-10,B点对应的数为70,可知线段AB=70-(-10)=80,80÷2=40,70-40=30,即线段AB的中点M所对应的数是30;
(2)设t秒后两只电子蚂蚁在点C相遇,则结合AB=80可得: ![]() ,由此可解得:
,由此可解得: ![]() ,则由此可得相遇时:BQ=16×2=32,由70-32=38可知,点C所对应的数是38;
,则由此可得相遇时:BQ=16×2=32,由70-32=38可知,点C所对应的数是38;
(3)本题要分两种情况讨论,①相遇前相距35个单位长度;②相遇后相距35个单位长度;由此设![]() 秒后两只电子蚂蚁相距35个单位长度,则由题意可得:①
秒后两只电子蚂蚁相距35个单位长度,则由题意可得:①![]() ,解得:
,解得: ![]() ;②
;②![]() ,解得:
,解得: ![]() ;当
;当![]() 时,点P所对应的数是:3×9-10=17;当
时,点P所对应的数是:3×9-10=17;当![]() 时,点P所对应的数是:3×23-10=59.
时,点P所对应的数是:3×23-10=59.
试题解析:
(1)∵点A对应的数为-10,B点对应的数为70,
∴AB=70-(-10)=80,
∵点M是AB的中点,
∴BM=80÷2=40,
∵70-40=30,
∴点M所对应的数是30;
(2)由(1)可知:AB=80,设t秒后P、Q相遇,
∴3t+2t=80,解得t=16;
∴此时点Q走过的路程为2×16=32,
∴此时C点表示的数为70﹣32=38.
答:C点对应的数是38;
(3)设![]() 秒后两只电子蚂蚁相距35个单位长度,则根据题意可得:
秒后两只电子蚂蚁相距35个单位长度,则根据题意可得:
①相遇前相距35个单位长度,则![]() ,解得:
,解得: ![]() ;
;
②相遇后相距35个单位长度,则![]() ,解得:
,解得: ![]() ;
;
即经过9秒或23秒,2只电子蚂蚁在数轴上相距35个单位长度;
当![]() 时,点P所对应的数是:3×9-10=17;
时,点P所对应的数是:3×9-10=17;
当![]() 时,点P所对应的数是:3×23-10=59.
时,点P所对应的数是:3×23-10=59.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品
篮球
排球
羽毛球拍
单价(元)
50
40
25
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A.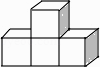
B.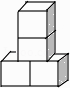
C.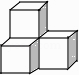
D.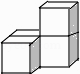
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠A=110°,E、F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC等于( )
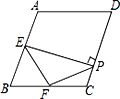
A. 45° B. 35° C. 55° D. 50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC于点E,则AE的长是( )
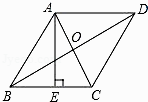
A.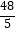 cm
cm
B.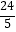 cm
cm
C.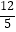 cm
cm
D.5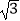 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )

A.4cm
B.3cm
C.2cm
D.1cm
相关试题

