【题目】如图,O为△ABC内一点,OD⊥AB于点D,OE⊥AC于点E,OF⊥BC于点F,若OD=OE=OF,连接OA,OB,OC,下列结论不一定正确的是( )
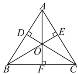
A. △BOD≌△BOF B. ∠OAD=∠OBF
C. ∠COE=∠COF D. AD=AE
参考答案:
【答案】B
【解析】
根据AAS推出△BOD≌△BOF和△COF≌△COE即可,由AO=AO,DO=EO根据勾股定理求出即可.
∵OD⊥AB,OE⊥AC,OF⊥BC,OD=OE=OF,
∴O在∠ABC的角平分线上(∠DBO=∠FBO),∠ODB=∠OFB=90°,
∵在△BOD和△BOF中
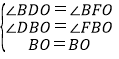
∴△BOD≌△BOF,正确,故本选项错误;
B、根据已知不能推出∠OAD=∠OBF,错误,故本选项正确;
C、∵OD⊥AB,OE⊥AC,OF⊥BC,OD=OE=OF,
∴O在∠ACB的角平分线上(∠FCO=∠ECO),∠OFC=∠OEC=90°,
∵在△COF和△COE中
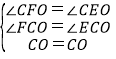
∴△COF≌△COE,
∴∠COE=∠COF,正确,故本选项错误;
D、∵OD⊥AB,OE⊥AC,
∴∠ADO=∠AEO=90°,
∵OD=OE,OA=OA,由勾股定理得:AE=AD,正确,故本选项错误;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示,且|a|=|c|.
(1)若|a+c|+|b|=2,求b的值;
(2)用“>”从大到小把a,b,﹣b,c连接起来.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一盒中有x个黑球和2个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,黑球的概率是
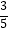 .
.
(1)填空:x=;
(2)从该盒子中随机摸出一个球,记下颜色后,不放回,再从该盒子中摸出一个球记下颜色,请用画树状图或列表求两次摸出的球的颜色都是白色的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】高速公路的同一侧有A、B两城镇,如图,它们到高速公路所在直线MN的距离分别为AA′=2 km,BB′=4 km,A′B′=8 km.要在高速公路上A′、B′之间建一个出口P,使A、B两城镇到P的距离之和最小.求这个最短距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点依次分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+1,+3,﹣6,﹣1,﹣2,+5.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:
+50,﹣15,+25,﹣10,﹣15,则该货车运送的水果总重量是多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
C类表示“听同学讲过”,D类表示“不知道”,划分类别后的数据整理如表:类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
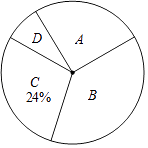
(1)表中的a=b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
相关试题

