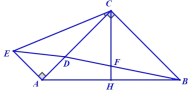
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CH为△ABC斜边上的中线,点F为CH上一点,连接BF并延长交AC于点D,过点A作AE⊥AC,连接CE和DE,若∠ACE=2∠ABF,CE=13,CD=8,则△CDE的面积为__________.
参考答案:
【答案】20
【解析】
延长BD交CE于G点,作![]() 交CE于K,交GD于O,设
交CE于K,交GD于O,设![]() ,则
,则![]() ,根据
,根据![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,可证
,可证![]() ,则
,则![]() ,根据ASA易证明
,根据ASA易证明![]() ,利用
,利用![]() ,
,![]() ,可证
,可证![]() ,可得
,可得![]() ,再利用三角形的面积公式即可求解.
,再利用三角形的面积公式即可求解.
解:如图示:延长BD交CE于G点,作![]() 交CE于K,交GD于O,
交CE于K,交GD于O,
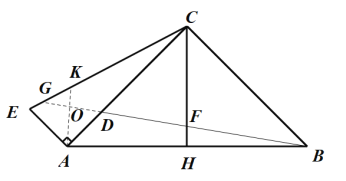
设![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]()
∴![]() ,
,
∴![]()
∴![]()
在Rt△ADO和Rt△BDC中,
![]() ,
,![]() ,
,
∴![]() ,则有
,则有![]()
在△CAK和△CGD中,
![]() ,
,![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
∴![]()
又∵![]()
即有![]() ,
,
∴![]()
∴![]() ,
,
故答案为:20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=
 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).
A. 1 B.
 C. 2 D.
C. 2 D. 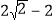
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)作出△ABC绕点A顺时针方向旋转90°后得到的△A1B1C1,并写出C1点的坐标 ;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,并求出△ABC的面积 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年植树节,东方红中学组织师生开展植树造林活动,为了了解全校800名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
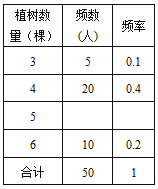
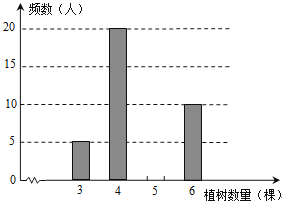
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的平均数;
(3)根据抽样数据,估计该校800名学生的植树数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。



-
科目: 来源: 题型:
查看答案和解析>>【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:(cos230°+sin230°)×tan60°
(2)解方程:x2﹣2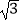 x﹣1=0.
x﹣1=0.
相关试题

