【题目】一辆快车从甲地开往乙地，一辆慢车从乙地开往甲地，两车同时出发，设慢车离乙地为y1（km），快车离乙地的距离为y2（km），慢车行驶时间为x（h），两车之间的距离为s（km），y1 ，y2与x的函数关系图像如图①所示，s与x的函数关系图如图②所示：

图① 图②

（1）图中的a= ，b= .

（2）求s关于x的函数关系式.

（3）甲、乙两地间有E、F两个加油站，相距200km，若慢车进入加油站E时，快车恰好进入加油站F，请直接写出加油站E到甲地的距离.

参考答案：

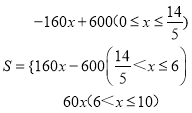【答案】（1）6； ；（2）；（3）加油站E到甲地的距离为300千米或450千米.

【解析】（1）根据S与x之间的函数关系式可以得到当位于C点时，两车之间的距离增加变缓，此时快车到站，指出此时a的值即可，求得a的值后求出两车相遇时的时间即为b的值；

（2）根据函数的图象可以得到A、B、C、D的点的坐标，利用待定系数法求得函数的解析式即可．

（3）分两车相遇前和两车相遇后两种情况讨论，当相遇前令s=200代入直线AB解析式，当相遇后令s=200代入直线BC解析式即可求得x的值．

解：(1)由S与x之间的函数的图象可知：当位于C点时，两车之间的距离增加变缓，

∴由此可以得到a=6，

∴快车每小时行驶100千米，慢车每小时行驶60千米，两地之间的距离为600，

∴b=600÷(100+60)= ；

(2)∵从函数的图象上可以得到A、B、C、D点的坐标分别为：(0,600)、(,0)、(6,360)、(10,600)，

∴设线段AB所在直线解析式为：S=kx+b，

∴ ，

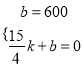解得：k=160，b=600，

设线段BC所在的直线的解析式为：S=kx+b，

∴

解得：k=160，b=600，

设直线CD的解析式为：S=kx+b，

∴，

解得：k=60，b=0

∴；

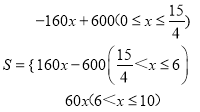(3)当两车相遇前分别进入两个不同的加油站，

此时：S=160x+600=200，

解得：x= ，

当两车相遇后分别进入两个不同的加油站，

此时：S=160x600=200，

解得：x=5，

∴当x=或5时，此时E加油站到甲地的距离为450km或300km.

关闭