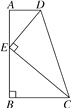
【题目】)如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.
(1)求证:△ADE∽△BEC;
(2)若AD=1,DE=![]() ,BC=2,求AB的长.
,BC=2,求AB的长.
参考答案:
【答案】(1)证明见解析;
(2) AB=2![]() .
.
【解析】试题分析:
(1)由已知易证∠A=∠B=∠DEC=90°,由此可证∠AED=∠BCE,从而可证△ADE∽△BEC;
(2)在Rt△ADE中,由勾股定理可得:AE=![]() =
=![]() ,再由△ADE∽△BEC利用相似三角形的性质可求得BE,最后由AB=AE+BE可求得AB的长.
,再由△ADE∽△BEC利用相似三角形的性质可求得BE,最后由AB=AE+BE可求得AB的长.
试题解析:
(1)∵AD∥BC,∠ABC=90°,
∴∠A=90°.
∵DE⊥CE,
∴∠DEC=90°,
∴∠AED+∠BEC=90°.
∵∠AED+∠ADE=90°,
∴∠ADE=∠BEC,
∴△ADE∽△BEC.
(2)在Rt△ADE中,AE=![]() =
=![]() .
.
∵△ADE∽△BEC,
∴![]() ,即
,即![]() ,
,
∴BE=![]() ,
,
∴AB=AE+BE=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上距离原点2个单位长度的点所表示的数是( )
A.2
B.﹣2
C.2或﹣2
D.1或﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算﹣3+(﹣1)的结果是( )
A.2
B.﹣2
C.4
D.﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)3ax2﹣6axy+3ay2
(2)(3x﹣2)2﹣(2x+7)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(x+5)(x﹣1)+(x﹣2)2
(2)(4ab3﹣8a2b2)÷4ab+(2a+b)(2a﹣b)
-
科目: 来源: 题型:
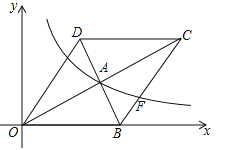
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数
 (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).(1)求反比例函数的表达式;
(2)求点F的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件衣服的进价为a,在进价的基础上增加20%标价,则标价可表示为( )
A.(1﹣20%)a
B.20%a
C.(1+20%)a
D.a+20%
相关试题

