【题目】如图,己知函数y=﹣ ![]() x+4的图象与坐标轴的交点分别为点A、B,点C与点B关于x轴对称,动点P、Q分别在线段BC、AB上(点P不与点B、C重合).且∠APQ=∠ABO
x+4的图象与坐标轴的交点分别为点A、B,点C与点B关于x轴对称,动点P、Q分别在线段BC、AB上(点P不与点B、C重合).且∠APQ=∠ABO
(1)点A的坐标为 , AC的长为;
(2)判断∠BPQ与∠CAP的大小关系,并说明理由;
(3)当△APQ为等腰三角形时,求点P的坐标.
参考答案:
【答案】
(1)(3,0),5
(2)解:∠BPQ=∠CAP.理由如下:
∵点C与点B关于x轴对称,
∴AB=AC,
∴∠ABC=∠ACB,
∵∠APQ=∠ABC,
∴∠ACB=∠APQ,
∵∠BPA=∠ACB+∠CAP,
即∠BPQ+∠APQ=∠ACB+∠CAP,
∴∠BPQ=∠CAP;
(3)解:当PA=PQ,如图1,则∠PQA=∠PAQ,
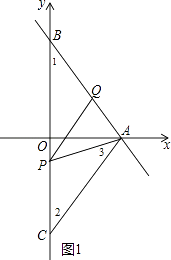
∵∠PQA=∠1+∠BPQ=∠APQ+∠BPQ=∠BPA,
∴BP=BA=5,
∴OP=BP﹣OB=1,
∴P(0,﹣1);
当AQ=AP,则∠AQP=∠APQ,
而∠AQP=∠BPA,所以此情况不存在;
当QA=QP,如图2,则∠APQ=∠PAQ,
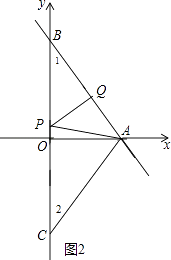
而∠1=∠APQ,
∴∠1=∠PAQ,
∴PA=PB,
设P(0,t),则PB=4﹣t,
∴PA=4﹣t,
在Rt△OPA中,∵OP2+OA2=PA2,
∴t2+32=(4﹣t)2,解得t= ![]() ,
,
∴P(0, ![]() ),
),
综上所述,满足条件的P点坐标为(0,﹣1),(0, ![]() ).
).
【解析】解:(1)当y=0时,﹣ ![]() x+4=0,解得x=3,则A(3,0),
x+4=0,解得x=3,则A(3,0),
当x=0时,y=﹣ ![]() x+4=4,则B(0,4),
x+4=4,则B(0,4),
∵点C与点B关于x轴对称,
∴C(0,﹣4),
∴AC= ![]() =5;
=5;
所以答案是(3,0),5;
【考点精析】本题主要考查了三角形的外角和勾股定理的概念的相关知识点,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
∵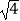 <
< 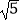 <
<  ,即2<
,即2< 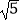 <3.
<3.
∴1<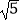 ﹣1<2
﹣1<2
∴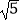 ﹣1的整数部分为1.
﹣1的整数部分为1.
∴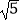 ﹣1的小数部分为
﹣1的小数部分为 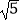 ﹣2.
﹣2.
解决问题:
已知a是 ﹣3的整数部分,b是
﹣3的整数部分,b是  ﹣3的小数部分,求(﹣a)3+(b+4)2的平方根.
﹣3的小数部分,求(﹣a)3+(b+4)2的平方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两台智能机器人从同一地点出发,沿着笔直的路线行走了450cm.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.两机器人行走的路程y(cm)与时间x(s)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
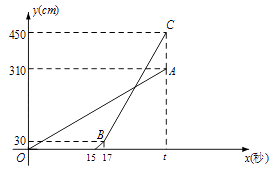
(1)乙比甲晚出发秒,乙提速前的速度是每秒cm,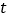 =;
=;
(2)已知甲匀速走完了全程,请补全甲的图象;
(3)当x为何值时,乙追上了甲? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列三条线段能构成三角形的是( )
A. 1,2,3B. 3,4,5C. 3,6,9,D. 3,7,4
-
科目: 来源: 题型:
查看答案和解析>>【题目】爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
时刻
9:00
9:45
12:00
碑上的数
是一个两位数,数字之和是9
十位与个位数字与9:00时所看到的正好相反
比9:00时看到的两位数中间多了个0
则小明在9:00时看到的两位数是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种花粉的质量约为 0.000 005 2kg,用科学记数法表示 0.0000052 是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式应提取公因式5a2b的是( )
A.15a2b﹣20a2b2
B.30a2b3﹣15ab4﹣10a3b2
C.10a2b﹣20a2b3+50a4b
D.5a2b4﹣10a3b3+15a4b2
相关试题

