【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球,其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相同,篮球与足球的单价各是多少元?
参考答案:
【答案】解:设足球的单价是 ![]() 元,则篮球的单价为(
元,则篮球的单价为( ![]() )元,依题意得:
)元,依题意得: ![]() ,方程两边乘x(x+40),得1500x=900x+36000,解得x=60,经检验,x=60是原分式方程的解,∴x+40=100(元).答:篮球的单价是100元,足球的单价是60元
,方程两边乘x(x+40),得1500x=900x+36000,解得x=60,经检验,x=60是原分式方程的解,∴x+40=100(元).答:篮球的单价是100元,足球的单价是60元
【解析】由“用1500元购进的篮球个数与900元购进的足球个数相同”得到等量关系,在由“篮球的单价比足球的单价多40元”得到两种球的数量关 系,得到方程。解分式方程后一定要记得检验。
【考点精析】通过灵活运用分式方程的应用,掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:
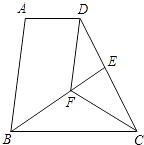
(1)△BFC≌△DFC;
(2)AD=DE. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
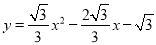 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.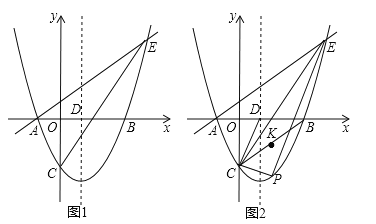
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线
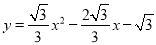 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
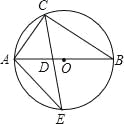
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A. 1:
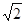 B. 1:
B. 1: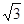 C. 1:2 D. 2:3
C. 1:2 D. 2:3 -
科目: 来源: 题型:
查看答案和解析>>【题目】正十边形的每个外角等于( )
A. 18° B. 36° C. 45° D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店将某种商品按进货价提高100%后,又以6折优惠售出,售价为60元,则这种商品的进货价是( )
A.120元
B.100元
C.72元
D.50元 -
科目: 来源: 题型:
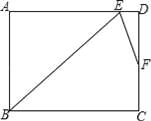
查看答案和解析>>【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)
相关试题

