【题目】已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P. 
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
参考答案:
【答案】
(1)证明:∵PQ⊥AQ,
∴∠AQP=90°=∠ABC,
在△APQ与△ABC中,
∵∠AQP=90°=∠ABC,∠A=∠A,
∴△AQP∽△ABC
(2)解:在Rt△ABC中,AB=3,BC=4,由勾股定理得:AC=5.
∵∠QPB为钝角,
∴当△PQB为等腰三角形时,
(i)当点P在线段AB上时,如题图1所示.
∵∠QPB为钝角,
∴当△PQB为等腰三角形时,只可能是PB=PQ,
由(1)可知,△AQP∽△ABC,
∴ ![]() ,即
,即 ![]() ,解得:PB=
,解得:PB= ![]() ,
,
∴AP=AB﹣PB=3﹣ ![]() =
= ![]() ;
;
(ii)当点P在线段AB的延长线上时,如题图2所示.
∵∠QBP为钝角,
∴当△PQB为等腰三角形时,只可能是PB=BQ.
∵BP=BQ,∴∠BQP=∠P,
∵∠BQP+∠AQB=90°,∠A+∠P=90°,
∴∠AQB=∠A,
∴BQ=AB,
∴AB=BP,点B为线段AP中点,
∴AP=2AB=2×3=6.
综上所述,当△PQB为等腰三角形时,AP的长为 ![]() 或6
或6
【解析】(1)由两对角相等(∠APQ=∠C,∠A=∠A),证明△AQP∽△ABC;(2)当△PQB为等腰三角形时,有两种情况,需要分类讨论.(i)当点P在线段AB上时,如题图1所示.由三角形相似(△AQP∽△ABC)关系计算AP的长;(ii)当点P在线段AB的延长线上时,如题图2所示.利用角之间的关系,证明点B为线段AP的中点,从而可以求出AP.
【考点精析】本题主要考查了等腰三角形的性质和直角三角形斜边上的中线的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形斜边上的中线等于斜边的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,如果直线l上依次有3个点A、B、C,那么

(1)在直线l上共有多少射线?多少条线段?
(2)在直线l上增加一个点,共增加了多少条射线?多少条线段?
(3)如果在直线l上增加到n个点,则共有多少条射线?多少条线段?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
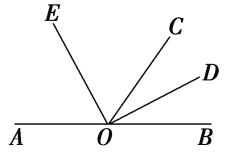
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是一个多面体的展开图,每个面上都标注了字母(字母均在外表面),请根据要求回答下列问题:
(1)如果面A在多面体的上面,那么哪一面在底部?
(2)如果面F在前面,从右面看是面B,那么哪一面在上面?
(3)如果从左面看是面C,面D在后面,那么哪一面在上面?

-
科目: 来源: 题型:
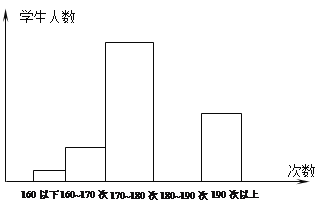
查看答案和解析>>【题目】为了解中学生的体能情况,某校抽取了50名八年级学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频数分布直方图如下图所示已知图中从左到右前第一、第二、第三、第五小组的频率分别为0.04 , 0.12 ,0.4 ,O.28 ,根据已知条件解答下列问题:
(1)第四个小组的频率是多少? 你是怎样得到的?
(2)这五小组的频数各是多少?
(3)在这次跳绳中,跳绳次数的中位数落在第几小组内?
(4)将频数分布直方图补全,并分别写出各个小组的频数,并画出频数分布折线图.
相关试题

