Question

【题目】有一枚均匀的正四面体，四个面上分别标有数字1，2，3，4，小红随机地抛掷一次，把着地一面的数字记为x；另有三张背面完全相同，正面上分别写有数字－2，－1，1的卡片，小亮将其混合后，正面朝下放置在桌面上，并从中随机地抽取一张，把卡片正面上的数字记为y；然后他们计算出S=x+y的值．

(1)用树状图或列表法表示出S的所有可能情况；

(2)分别求出当S=0和S<2时的概率．

Answer 1

【答案】（1）答案见解析；（2），

【解析】试题分析：列举出符合题意的各种情况的个数，再根据概率公式解答即可．

解：(1)画树状图,

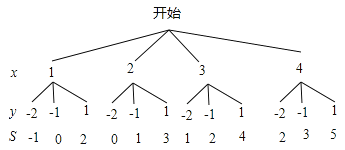
(2)由图可知，所有可能出现的结果有12种，其中S=0的有2种，S<2的有5种，

∴P(S=0)= ,

P(S<2)= .