【题目】某商场准备购进两种型号的摩托车共25辆,预计投资10万元.现有甲、乙、丙三种摩托车,甲种每辆4200元,可获利400元;乙种每辆3700元,可获利350元;丙种每辆3200元,可获利320元,且10万元资本全部用完.
(1)请你帮助该商场设计进货方案;
(2)从销售利润上考虑,应选择哪种方案?
参考答案:
【答案】(1)进货方案有两种:①甲种进15辆,乙种进10辆;②甲种进20辆,乙种进5辆;(2)从销售利润上看要选择方案2.
【解析】试题分析:(1)分当购进甲、乙两种型号的摩托车;购进甲、丙两种型号的摩托车;购进乙、丙两种型号的摩托车三种情况.并分别通过设出未知数,解二元一次方程组来解答.
(2)根据(1)的结论求出每种近货方案的利润,选择利润最大的那种方案就可以了.
试题解析:解:(1)设购进甲种摩托车x辆,乙种摩托车y辆,则
![]() ,解得:
,解得:![]() ;
;
设购进甲种摩托车m辆,丙种摩托车n辆,则
![]() ,解得:
,解得:![]() ;
;
设购进乙种摩托车a辆,丙种摩托车b辆,则
![]() ,解得:
,解得:![]() (不符合题意,舍去)
(不符合题意,舍去)
故进货方案有两种:①甲种摩托车进15辆,乙种摩托车进10辆;②甲种摩托车进20辆,丙种摩托车进5辆.
(2)由(1)得,方案1的销售利润为:400×15+350×10=9500元;
方案2的销售利润为:400×20+320×5=9600元.
∵9600元>9500元,∴从销售利润上看要选择方案2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:

(2)如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.

-
科目: 来源: 题型:
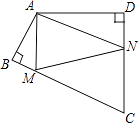
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
A.130°
B.120°
C.110°
D.100° -
科目: 来源: 题型:
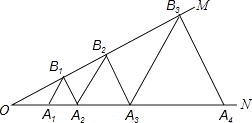
查看答案和解析>>【题目】图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数1,0,﹣1,|﹣2|中,最小的数是 .
-
科目: 来源: 题型:
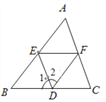
查看答案和解析>>【题目】如图,(1)如果∠1=__________,那么DE∥AC;(同位角相等,两直线平行);
(2)如果∠1=__________,那么EF∥BC;(内错角相等,两直线平行);
(3)如果∠DEF+__________=180°,那么DE∥AC;(同旁内角互补,两直线平行);
(4)如果∠2+__________=180°,那么AB∥DF;(同旁内角互补,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是必然事件的是( )
A.3个人分成两组,并且每组必有人,一定有2个人分在一组
B.抛一枚硬币,正面朝上
C.随意掷两个均匀的骰子,朝上面的点数之和为6
D.打开电视,正在播放动画片
相关试题

