【题目】在平面直角坐标系xOy中，已知点P（3，0），⊙P是以点P为圆心，2为半径的圆，若一次函数y=kx+b的图象过点A（﹣1，0）且与⊙P相切，则k+b的值为 ．

参考答案：

【答案】±
【解析】解：根据题意画出相应的图形，如图所示：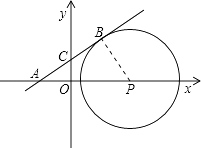
当直线AB与圆P相切，设切点为B点，且切点B在第一象限时，
连接PB，由AB为圆P的切线，得到BP⊥AB，
又∵A（﹣1，0），P（3，0），
∴OA=1，OP=3，又BP=2，
则AP=OA+OP=1+3=4，
在Rt△ABP中，BP= AP，
可得出∠BAP=30°，
在Rt△ACO中，OA=1，∠BAP=30°，
∴tan∠BAP=tan30°= =OC，
∴OC= ，即C（0， ），
设直线AC的解析式为y=kx+b，将A和C的坐标代入得：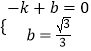
，
解得： ，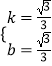
∴k+b= ；
当直线AB与圆P相切时，切点B在第四象限时，同理得到k=b=﹣ ，
可得k+b=﹣ ，
综上，k+b=± ．
所以答案是：± ．
【考点精析】关于本题考查的确定一次函数的表达式和切线的性质定理，需要了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案．

关闭