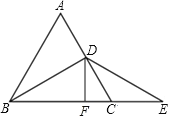
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,

(1)求证:DB=DE.
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
参考答案:
【答案】(1)证明见解析(2)48
【解析】试题分析:(1)根据等边三角形的性质得到∠ABC=∠ACB=60°,∠DBC=30°,再根据角之间的关系求得∠DBC=∠CED,根据等角对等边即可得到DB=DE;(2)根据直角三角形中,30°的锐角所对的直角边等于斜边的一半DC=8,AC=16,即可求得△ABC的周长.
试题解析:
(1)证明:∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=![]() ∠BCD=30°.
∠BCD=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边);
(2)解: ∵∠CDE=∠CED=![]() ∠BCD=30°,
∠BCD=30°,
∴∠CDF=30°,
∵CF=4,
∴DC=8,
∵AD=CD,
∴AC=16,
∴△ABC的周长=3AC=48.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 问题与探索
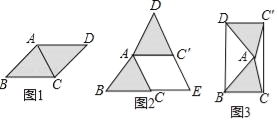
问题情境:课堂上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图(1),将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现:
(1)将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图(2)所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是 .
(2)创新小组将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图(3)所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形,请证明这个结论.
-
科目: 来源: 题型:
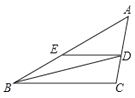
查看答案和解析>>【题目】BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=72°,求∠BED的度数.
-
科目: 来源: 题型:
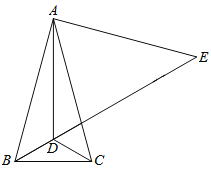
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=30°,点D是△ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.
(1)求∠ADE的度数;
(2)求证:DE=AD+DC;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某日天气预报说今天 最高气温为8℃,气温的极差为9℃,则该日最低气温为_____________℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=kx﹣1(常数k>0)的图象不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名运动员,在相同情况下各射击10次.两名的平均数都是8, 方差分别为4.2.2,则成绩较好的是__________________.
相关试题

