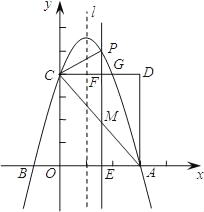
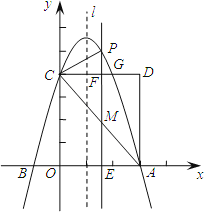
【题目】如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4;(2)PM=﹣
x+4;(2)PM=﹣![]() m2+4m(0<m<3);(3)存在这样的点P使△PFC与△AEM相似,此时m的值为
m2+4m(0<m<3);(3)存在这样的点P使△PFC与△AEM相似,此时m的值为![]() 或1,△PCM为直角三角形或等腰三角形.
或1,△PCM为直角三角形或等腰三角形.
【解析】试题分析:(1)将A(3,0),C(0,4)代入y=ax2-2ax+c,运用待定系数法即可求出抛物线的解析式;
(2)先根据A、C的坐标,用待定系数法求出直线AC的解析式,进而根据抛物线和直线AC的解析式分别表示出点P、点M的坐标,即可得到PM的长;
(3)由于∠PFC和∠AEM都是直角,F和E对应,则若以P、C、F为顶点的三角形和△AEM相似时,分两种情况进行讨论:①△PFC∽△AEM,②△CFP∽△AEM;可分别用含m的代数式表示出AE、EM、CF、PF的长,根据相似三角形对应边的比相等列出比例式,求出m的值.
试题解析:(1)∵抛物线y=ax2-2ax+c(a≠0)经过点A(3,0),点C(0,4),
∴![]() ,
,
解得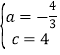 .
.
∴抛物线的解析式为y=-![]() x2+
x2+![]() x+4;
x+4;
(2)设直线AC的解析式为y=kx+b,
∵A(3,0),点C(0,4),
∴![]() ,
,
解得 .
.
∴直线AC的解析式为y=-![]() x+4.
x+4.
∵点M的横坐标为m,点M在AC上,
∴M点的坐标为(m,-![]() m+4),
m+4),
∵点P的横坐标为m,点P在抛物线y=-![]() x2+
x2+![]() x+4上,
x+4上,
∴点P的坐标为(m,-![]() m2+
m2+![]() m+4),
m+4),
∴PM=PE-ME=(-![]() m2+
m2+![]() m+4)-(-
m+4)-(-![]() m+4)=-
m+4)=-![]() m2+4m,
m2+4m,
即PM=-![]() m2+4m(0<m<3);
m2+4m(0<m<3);
(3)在(2)的条件下,连结PC,在CD上方的抛物线部分存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似.理由如下:由题意,可得AE=3-m,EM=-![]() m+4,CF=m,若以P、C、F为顶点的三角形和△AEM相似,情况:
m+4,CF=m,若以P、C、F为顶点的三角形和△AEM相似,情况:
①P点在CD上方,则PF=-![]() m2+
m2+![]() m+4-4=-
m+4-4=-![]() m2+
m2+![]() m.
m.
若△PFC∽△AEM,则PF:AE=FC:EM,
即(-![]() m2+
m2+![]() m):(3-m)=m:(-
m):(3-m)=m:(-![]() m+4),
m+4),
∵m≠0且m≠3,
∴m=![]() ;
;
②若△CFP∽△AEM,则CF:AE=PF:EM,
即m:(3-m)=(-![]() m2+
m2+![]() m):(-
m):(-![]() m+4),
m+4),
∵m≠0且m≠3,
∴m=1.
综上所述,存在这样的点P使△PFC与△AEM相似.此时m的值为![]() 或1.
或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,某家快递公司,今年三月份与五月份完成投递的快件总件数分别是5万件和
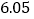 万件,现假定该公司每月投递的快件总件数的增长率相同.
万件,现假定该公司每月投递的快件总件数的增长率相同.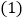 求该公司投递快件总件数的月平均增长率;
求该公司投递快件总件数的月平均增长率; 如果平均每人每月可投递快递
如果平均每人每月可投递快递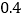 万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务?
万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
-
科目: 来源: 题型:
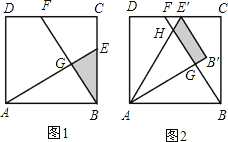
查看答案和解析>>【题目】已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
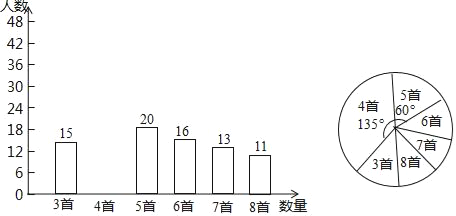
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
10
10
15
40
25
20
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直立于地面上的电线杆
 ,在阳光下落在水平地面和坡面上的影子分别是
,在阳光下落在水平地面和坡面上的影子分别是 .测得
.测得 ,
,  ,
,  ,在D处测得电线杆顶端A的仰角为
,在D处测得电线杆顶端A的仰角为 ,则电线杆
,则电线杆 的高度为( )
的高度为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C,D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨:从B城往C,D两乡运肥料的费用分别为15元/吨和24元/吨,现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求y与x的函数关系式.
(3)怎样调运才能使总运费最少?并求最少运费.
相关试题

