搜索
【题目】解不等式（组），并在数轴上表示它的解集
（1）2（1+x）＜3；
（2）
.
参考答案：
【答案】（1）x
，该不等式的解集在数轴上表示见解析；（2）x≥6，不等式组的解集在数轴上表示见解析.
【解析】
（1）按照去括号、移项、合并同类项、系数化为1的步骤求出解集，然后画数轴表示即可；
（2）先分别解两个不等式，求出它们的解集，再求两个不等式解集的公共部分即可得到不等式组的解集，再画数轴表示即可.
（1）去括号得：2+2x＜3，
移项得：2x＜3﹣2，
合并同类项得：2x＜1，
系数化为1得：x＜
，
即不等式的解集为：x，
该不等式的解集在数轴上表示如下：
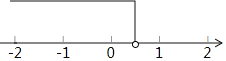
（2）解不等式2x+3≥x+9得：x≥6，
解不等式
＞2﹣x得：x
，
即不等式组的解集为：x≥6，
不等式组的解集在数轴上表示如下：
-
科目： 来源： 题型：
查看答案和解析>>【题目】为落实“绿水青山就是金山银山”的发展理念，某县政府部门决定，招标一工程队负责完成一座水库的土方施工任务．该工程队有A，B两种型号的挖掘机，已知1台A型和2台B型挖掘机同时施工1小时共挖土80立方米，2台A型和3台B型挖掘机同时施工1小时共挖土140立方米．每台A型挖掘机一个小时的施工费用是350元，每台B型挖掘机一个小时的施工费用是200元．
（1）分别求每台A型，B型挖掘机一小时各挖土多少立方米？
（2）若A型和B型挖掘机共10台同时施工4小时，至少完成1360立方米的挖土量，且总费用不超过14000元．问施工时有哪几种调配方案？且指出哪种调配方案的施工费用最低，最低费用多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，在△ABC中，∠A
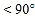，P是BC边上的一点，
，
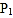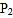是点P关于AB、AC的对称点，连结
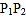，分别交AB、AC于点D、E. ①若
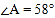，求
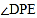的度数； ②请直接写出∠A与
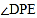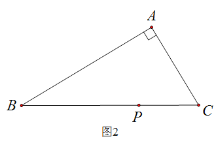
的数量关系：___________________________； （2）如图2，在△ABC中，若∠BAC
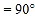，用三角板作出点P关于AB、AC的对称点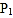、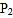，（不写作法，保留作图痕迹），试判断点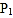，与点A是否在同一直线上，并说明理由. 
-
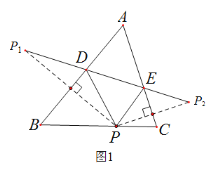
科目： 来源： 题型：
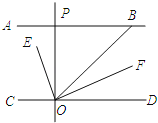
查看答案和解析>>【题目】如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO＝40°，则下列结论：①∠BOE＝70°；②OF平分∠BOD；③∠POE＝∠BOF；④∠POB＝2∠DOF．其中正确结论有_____填序号）
-
科目： 来源： 题型：
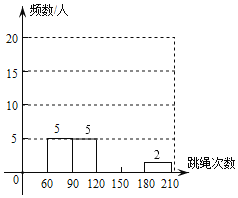
查看答案和解析>>【题目】学校为了了解七年学生跳绳情况，从七年级学生中随机抽查了50名学生进行1分钟跳绳测试，并对测试结果统计后绘制了如下不完整统计图表，请根据图表中的信息解答下列问题．
组别
次数
频数（人）
百分比
1
60≤x＜90
5
10%
2
90≤x＜120
5
b
3
120≤x＜150
18
36%
4
150≤x＜180
a
c
5
180≤x＜210
2
4%
合计
50
1
（1）直接写出a＝ ，b＝ ，c＝ ；
（2）请补全频数分布直方图；
（3）若该校七年级共有学生400人，请你估计该校七年级学生跳绳次数在90≤x＜150范围的学生约有多少人？（
-
科目： 来源： 题型：
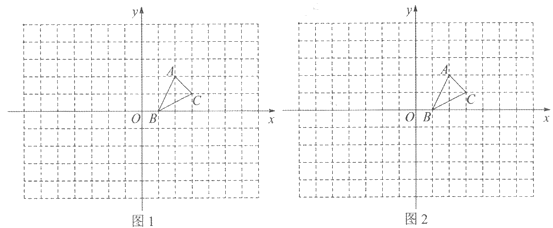
查看答案和解析>>【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）
（1）在图l中画出△ABC关于x轴对称的△A1B1C1；
（2）在图2中，以点O为位似中心，将△ABC放大，使放大后的△A2B2C2与△ABC的对应边的比为2：1（画出一种即可）. 直接写出点A的对应点A2的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，一次函数y=x+2的图象与反比例函数y=
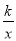的图象交于A、B两点，且点A的坐标为（1，m）. （1）求反比例函数y=
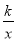的表达式；（2）点C（n，1）在反比例函数y=
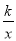的图象上，求△AOC的面积.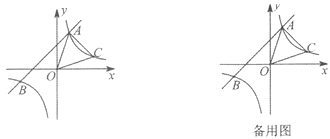 
相关试题
