【题目】金秋十月,丹桂飘香,重庆双福育才中学迎来了首届行知创新科技大赛,初二年级某班共有18人报名参加航海组,航空组和无人机组三个项目组的比赛(每人限参加一项),其中航海组的同学比无人机组的同学的两倍少3人,航空组的同学不少于3人但不超过9人,班级决定为航海组的每位同学购买2个航海模型,为航空组的每位同学购买3个航空模型,为无人机组的每位同学购买若干个无人机模型,已知航海模型75元每个,航空模型98元每个,无人机模型165元每个,若购买这三种模型共需花费6114元,则其中购买无人机模型的费用是__________.
参考答案:
【答案】3300元
【解析】
设无人机组有x个同学,航空组有y个同学,根据人数为18列出二元一次方程,根据航空组的同学不少于3人但不超过9人,得到x,y的解,再代入模型费用进行验证即可求解.
设无人机组有x个同学,航空组有y个同学,
依题意得x+2x-3+y=18
解得x=![]()
∵航空组的同学不少于3人但不超过9人,x,y为正整数,
故方程的解为![]() ,
,![]() ,
,![]()
设为无人机组的每位同学购买a个无人机模型,
当![]() 时,依题意得6a×165+2×9×75+3×3×98=6114
时,依题意得6a×165+2×9×75+3×3×98=6114
解得a=![]() ,不符合题意;
,不符合题意;
当![]() 时,依题意得5a×165+2×7×75+6×3×98=6114
时,依题意得5a×165+2×7×75+6×3×98=6114
解得a=4,符合题意,故购买无人机模型的费用是3300元;
当![]() 时,依题意得4a×165+2×5×75+9×3×98=6114
时,依题意得4a×165+2×5×75+9×3×98=6114
解得a=![]() ,不符合题意;
,不符合题意;
综上,答案为3300元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)已知直线l的解析式为y=kx﹣5.
(1)求抛物线L1的解析式、对称轴和顶点坐标.
(2)若直线l将线段AB分成1:3两部分,求k的值;
(3)当k=2时,直线与抛物线交于M、N两点,点P是抛物线位于直线上方的一点,当△PMN面积最大时,求P点坐标,并求面积的最大值.
(4)将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方,将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围;
②直接写出直线l与图象L2有四个交点时k的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线c1:
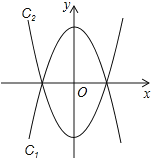
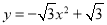 沿x轴翻折,得到抛物线c2,如图1所示.
沿x轴翻折,得到抛物线c2,如图1所示.(1)请直接写出抛物线c2的表达式;
(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与
 轴的交点从左到右依次为D、E.
轴的交点从左到右依次为D、E.①当B、D是线段AE的三等分点时,求m的值;
②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
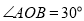 ,
,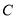 是
是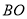 上的一点,
上的一点,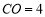 ,点
,点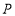 为
为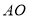 上的一动点,点
上的一动点,点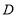 为
为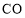 上的一动点,则
上的一动点,则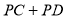 的最小值为 ________,当
的最小值为 ________,当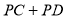 的值取最小值时,则
的值取最小值时,则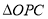 的面积为________.
的面积为________.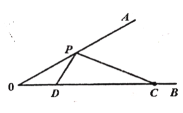
-
科目: 来源: 题型:
查看答案和解析>>【题目】奉节脐橙是重庆市奉节县特产,中国地理标志产品,眼下,正值奉节脐橙销售旺季,某商家看准商机,第一次用4800元购进一批奉节脐橙,销售良好,于是第二次又用12000元购进一批奉节脐橙,但此时进价比第一次涨了2元,所购进的数量恰好是第一次购进数量的两倍.
(1)求第一次购进奉节脐橙的进价.
(2)实际销售中,两次售价均相同,在销售过程中,由于消费者挑选后,果品下降,第一批奉节脐橙的最后100千克八折售出,第二批奉节脐橙的最后800千克九折售出,若售完这两批奉节脐橙的获利不低于9400元,则售价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 +bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
+bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.(1)求抛物线解析式;
(2)若线段DE是CD绕点D顺时针旋转90°得到,求线段DF的长;
(3)若线段DE是CD绕点D旋转90°得到,且点E恰好在抛物线上,请求出点E的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
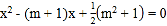 有实数根.
有实数根.(1)求m的值;
(2)先作
 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求
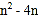 的最大值和最小值.
的最大值和最小值.
相关试题

