【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )

A. 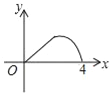 B.
B. 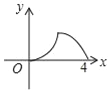 C.
C.  D.
D. 
参考答案:
【答案】B
【解析】过A点作AH⊥BC于H,利用等腰直角三角形的性质得到∠B=∠C=45°,BH=CH=AH=![]() BC=2,分类讨论:当0≤x≤2时,如图1,易得PD=BD=x,根据三角形面积公式得到y=
BC=2,分类讨论:当0≤x≤2时,如图1,易得PD=BD=x,根据三角形面积公式得到y=![]() x2;当2<x≤4时,如图2,易得PD=CD=4﹣x,根据三角形面积公式得到y=﹣
x2;当2<x≤4时,如图2,易得PD=CD=4﹣x,根据三角形面积公式得到y=﹣![]() x2+2x,于是可判断当0≤x≤2时,y与x的函数关系的图象为开口向上的抛物线的一部分,当2<x≤4时,y与x的函数关系的图象为开口向下的抛物线的一部分,然后利用此特征可对四个选项进行判断.
x2+2x,于是可判断当0≤x≤2时,y与x的函数关系的图象为开口向上的抛物线的一部分,当2<x≤4时,y与x的函数关系的图象为开口向下的抛物线的一部分,然后利用此特征可对四个选项进行判断.
解:过A点作AH⊥BC于H,
∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,BH=CH=AH=![]() BC=2,
BC=2,
当0≤x≤2时,如图1,
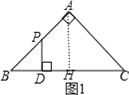
∵∠B=45°,
∴PD=BD=x,
∴y=![]() xx=
xx=![]() x2;
x2;
当2<x≤4时,如图2,
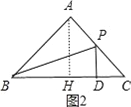
∵∠C=45°,
∴PD=CD=4﹣x,
∴y=![]() (4﹣x)x=﹣
(4﹣x)x=﹣![]() x2+2x,
x2+2x,
故选B.
“点睛”本题主要考查了动点问题的函数图象,解题时注意:二次函数的图象为抛物线,一次函数的图象为直线,用图象解集问题时,要理清图象的含义即会识图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下四个结论:①△ACD≌△BCE;②△CDP≌△CEQ;③PQ∥AE;④∠AOB=60°.一定成立的结论有(把你认为正确结论的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:m6m3的结果( )
A.m18
B.m9
C.m3
D.m2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个多边形的内角和是它外角和的5倍,则这个多边形是边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两商场以同样价格出售同样的商品.在甲商场累计购物超过100元后,超出100元的部分按八折收费;在乙商场累积购物超过50元后,超过50元的部分按九折收费.李红累计购物超过100元,当李红的累计购物金额超过_____元时,在甲商场购物花费少.
相关试题

