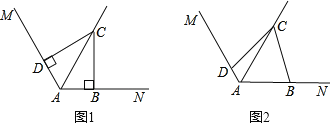
【题目】已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
参考答案:
【答案】(1)AD+AB=AC;(2)仍成立.
【解析】
(1)得到∠ACD=∠ACB=30°后再可以证得AD=AB![]() AC从而,证得结论;
AC从而,证得结论;
(2)过点C分别作AM、AN的垂线,垂足分别为E、F,证得△CED≌△CFB后即可得到AD+AB=AE﹣ED+AF+FB=AE+AF,从而证得结论.
(1)关系是:AD+AB=AC.证明如下:
∵AC平分∠MAN,∠MAN=120°,∴∠CAD=∠CAB=60°.
又∵∠ADC=∠ABC=90°,∴∠ACD=∠ACB=30°,则AD=AB![]() AC(直角三角形一锐角为30°,则它所对直角边为斜边一半),∴AD+AB=AC.
AC(直角三角形一锐角为30°,则它所对直角边为斜边一半),∴AD+AB=AC.
(2)仍成立.理由如下:
过点C分别作AM、AN的垂线,垂足分别为E、F.
∵AC平分∠MAN,∴CE=CF(角平分线上点到角两边距离相等).
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,∴∠CDE=∠ABC.
又∵∠CED=∠CFB=90°,∴△CED≌△CFB(AAS).
∵ED=FB,∴AD+AB=AE﹣ED+AF+FB=AE+AF.
由(1)知AE+AF=AC,∴AD+AB=AC.
-
科目: 来源: 题型:
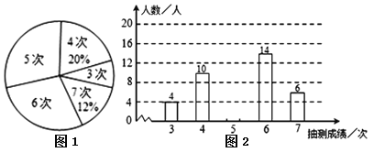
查看答案和解析>>【题目】为了解某校八年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2两幅尚不完整的统计图.
(1)本次抽测的男生有 人,抽测成绩的众数是 ;
(2)请你将图2的统计图补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校400名八年级男生中估计有多少人体能达标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“保护环境,人人有责”,为了更好的利用水资源,某污水处理厂决定购买
 、
、 两型号污水处理设备共10台,其信息如下表.(1)设购买
两型号污水处理设备共10台,其信息如下表.(1)设购买 型设备
型设备 台,所需资金共为
台,所需资金共为 万元,每月处理污水总量为
万元,每月处理污水总量为 吨,试写出
吨,试写出 与
与 之间的函数关系式,
之间的函数关系式, 与
与 之间的函数关系式;(2)经预算,该污水处理厂购买设备的资金不超过88万元, 每月处理污水总量不低于2080吨,请你列举出所有购买方案,并指出哪种方案最省钱,需多少资金?
之间的函数关系式;(2)经预算,该污水处理厂购买设备的资金不超过88万元, 每月处理污水总量不低于2080吨,请你列举出所有购买方案,并指出哪种方案最省钱,需多少资金?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小明:那直角三角形是否存在奇异三角形呢?
小红:等边三角形一定是奇异三角形.
(1)根据“奇异三角形”的定义,小红得出命题:“等边三角形一定是奇异三角形”,则小红提出的命题是 .(填“真命题”或“假命题”)
(2)若
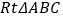 是奇异三角形,其中两边的长分别为
是奇异三角形,其中两边的长分别为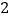 、
、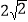 ,则第三边的长为 .
,则第三边的长为 .(3)如图,
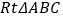 中,
中,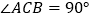 ,以
,以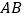 为斜边作等腰直角三角形
为斜边作等腰直角三角形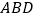 ,点
,点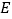 是
是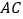 上方的一点,且满足
上方的一点,且满足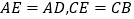 .求证:
.求证: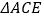 是奇异三角形.
是奇异三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(甲),在正方形
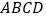 中,
中, 是
是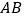 上一点,
上一点,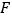 是
是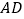 延长线上一点,且
延长线上一点,且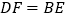 .
.(1)求证:
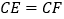 ;
;(2)在如图(甲)中,若
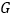 在
在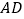 上,且
上,且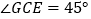 ,则
,则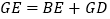 成立吗?
成立吗?证明你的结论.(3)运用(1)(2)解答中积累的经验和知识,完成下题:
如图(乙)四边形
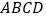 中,
中,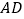 ∥
∥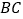 (
(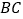 >
>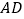 ),
),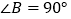 ,
,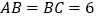 ,点
,点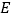 是
是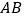 上一点,且
上一点,且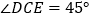 ,
,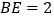 ,求
,求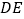 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 某公园准备修建一块长方形草坪,长为a米,宽为b米.并在草坪上修建如图所示的十字路,
已知十字路宽2米.
(1)用含a、b的代数式表示修建的十字路的面积.
(2)若a=30,b=20,求草坪(阴影部分)的面积.
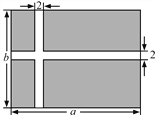
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并解答问题:
数学大师的名题与方程
欧拉是18世纪瑞士著名的数学大师.他的一生都致力于数学各个领域的研究,并取得非凡的成就.在他所著的《代数学入门》一书中就曾经出现过好几道和遗产分配有关的数学问题.他构思这些问题的初衷,正是为了强化方程解题的适用和便利.
请用适当的方法解答下面问题:
父亲死后,四个儿子按下述方式分了他的财产:老大拿了财产的一半少3000英镑:老二拿了财产的
 少1000英镑;老三拿了恰好是财产的
少1000英镑;老三拿了恰好是财产的 ;老四拿了财产的
;老四拿了财产的 加上600英镑.问整个财产有多少?每个儿子各分了多少?
加上600英镑.问整个财产有多少?每个儿子各分了多少?
相关试题

