【题目】2017年某企业按餐厨垃圾处理费25元/ 吨、建筑垃圾处理费16元/ 吨的收费标准,共支付餐厨和建筑垃圾处理费5200元.从2018年元月起,收费标准上调为:餐厨垃圾处理费100元/ 吨,建筑垃圾处理费30元/ 吨.若该企业2018年处理的这两种垃圾数量与2017年相比没有变化,就要多支付垃圾处理费8800元.
(1)该企业2017年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2018年将上述两种垃圾处理总量减少到240吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2018年该企业最少需要支付餐厨垃圾处理费多少元?
参考答案:
【答案】(1) 该企业2017年处理的餐厨垃圾80吨,建筑垃圾200吨;(2) 2018年该企业最少需要支付餐厨垃圾处理费共6000元.
【解析】
(1)设该企业2017年处理餐厨垃圾x吨,建筑垃圾y吨,根据等量关系:2017年餐厨垃圾处理费+建筑垃圾处理费=5200元和2018年餐厨垃圾处理费+建筑垃圾处理费=5200+8800(元)列出方程组,解方程组即可求得所求答案;
(2)设该企业2018年处理餐厨垃圾a吨,则由题意可得2018年该企业处理了建筑垃圾(240-a)吨,根据不等关系“建筑垃圾处理量不超过餐厨垃圾处理量的3倍”列出不等式即可求得该企业2018年处理餐厨垃圾的最少量,由此即可求出2018年该企业最少需要支付的餐厨垃圾处理费的值.
(1)设该企业2017年处理的餐厨垃圾x吨,建筑垃圾y吨,根据题意,得
![]() ,
,
解得![]() .
.
答:该企业2017年处理的餐厨垃圾80吨,建筑垃圾200吨;
(2)设该企业2018年处理的餐厨垃圾a吨,建筑垃圾(240-a)吨,根据题意得,
![]() ,
,
解得![]() ,即2018年该企业处理的餐厨垃圾最少有60吨,
,即2018年该企业处理的餐厨垃圾最少有60吨,
∴当a=60时,2018年需要支付的餐厨垃圾处理费最少,最少费用=60×100=6000(元).
答:2018年该企业最少需要支付餐厨垃圾处理费共6000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期日晚饭后,小红从家里出去散步,如图所示,描述了她散步过程中离家的距离s(m)与散步所用的时间t(min)之间的函数关系,该图象反映的过程是:小红从家出发,到了一个公共阅报栏,看了一会报后,继续向前走了一段,在邮亭买了一本杂志,然后回家了.依据图象回答下列问题

(1)公共阅报栏离小红家有______米,小红从家走到公共阅报栏用了______分;
(2)小红在公共阅报栏看新闻一共用了______分;
(3)邮亭离公共阅报栏有______米,小红从公共阅报栏到邮亭用了______分;
(4)小红从邮亭走回家用了______分,平均速度是______米/秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下面的图象记录了某地一月份某大的温度随时间变化的情况,请你仔细观察图象回答下面的问题:

(1)在这个问题中,变量分别是______,时间的取值范围是______;
(2)20时的温度是______℃,温度是0℃的时刻是______时,最暖和的时刻是_______时,温度在-3℃以下的持续时间为______小时;
(3)你从图象中还能获得哪些信息?(写出1~2条即可)
答:__________________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家知道,函数图象特征与函数性质之间存在着必然联系.请根据图中的函数图象特征及表中的提示,说出此函数的变化规律.此外,你还能说出此函数的哪些性质?
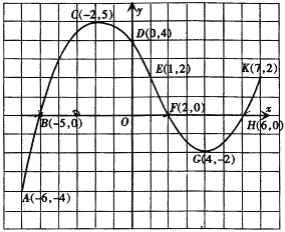
序号
函数图象特征
函数变化规律
(1)
曲线从点A(-6,-4)至点K(7,2)
自变量的取值范围是______.
(2)
曲线与y轴交于点D(0,4)
当x=______时,y=______.
(3)
曲线与x轴分别交于点B(-5,0)、F(2,0)、H(6,0)
当x的值分别为______时,y=0.
(4)
曲线经过点E(1,2)
当x=______时,y=______.
(5)
由左至右曲线AC呈上升状态
当-6≤x≤-2时,y随x的增大而______.
(6)
由左至右曲线CG呈下降状态
当______时,y随x的增大而___________.
(7)
由左至右曲线GK呈____________
当______时y随____________.
(8)
曲线上的最高点是C(-2,5)
当x=______时,y有______值,且这个值为____________.
(9)
曲线上的最低点是____________
当x=______时,y有______值,且这个值为____________.
(10)
曲线BCF位于x轴的上方
当______时,y______0.
-
科目: 来源: 题型:
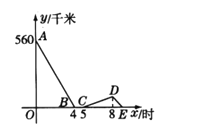
查看答案和解析>>【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后停留一段时间,然后分别按原速一同驶往甲地后停车。设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲、乙两地之间的距离为________千米;
(2)求快车和慢车的速度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是( )

A.
B.1
C.
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正偶数按照图中所示的规律排列下去,若用有序实数对(a,b)表示第a行的第b个数.如(3,2)表示偶数10.
(1)图中(8,4)的位置表示的数是________,偶数42对应的有序实数对是________
(2)第n行的最后一个数用含n的代数式表示为________,并简要说明理由.

相关试题

