【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)若数![]() 没有平方根,判断点
没有平方根,判断点![]() 在第几象限并说明理由;
在第几象限并说明理由;
(2)若点![]() 到
到![]() 轴的距离是点
轴的距离是点![]() 到
到![]() 轴的距离的2倍,求点
轴的距离的2倍,求点![]() 的坐标;
的坐标;
(3)若点![]() 的坐标为
的坐标为![]() ,三角形
,三角形![]() 的面积是三角形
的面积是三角形![]() 面积的3倍,求点
面积的3倍,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1) 点A在第二象限;(2) (![]() ,
,![]() )或(
)或(![]() ,
,![]() ); (3) (
); (3) (![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)根据平方根的意义得到![]() ,然后根据各象限点的坐标特征可判断点A在第二象限;
,然后根据各象限点的坐标特征可判断点A在第二象限;
(2)先利用方程组,用![]() 表示
表示![]() 、
、![]() 得
得![]() ,
,![]() ,则B点坐标为(
,则B点坐标为(![]() ,
,![]() ),再利用点A到
),再利用点A到![]() 轴的距离是点B到
轴的距离是点B到![]() 轴距离的2倍得到
轴距离的2倍得到![]() ,则
,则![]() 或
或![]() ,分别解方程求出
,分别解方程求出![]() 的值,于是可求出B点坐标;
的值,于是可求出B点坐标;
(3)利用A(![]() ,
,![]() )和B(
)和B(![]() ,
,![]() )得到AB与
)得到AB与![]() 轴平行,由于点D的坐标为(2,
轴平行,由于点D的坐标为(2,![]() ),△OAB的面积是△DAB面积的3倍,则判断点A、点B在
),△OAB的面积是△DAB面积的3倍,则判断点A、点B在![]() 轴的下方,即
轴的下方,即![]() ,根据三角形面积公式即可求得
,根据三角形面积公式即可求得![]() 的值,于是可求出B点坐标.
的值,于是可求出B点坐标.
(1)∵![]() 没有平方根,
没有平方根,
∴![]() ,
,
∴![]() ,
,
∴点A在第二象限;
(2)解方程组![]() ,用
,用![]() 表示
表示![]() 、
、![]() 得
得![]() ,
,![]() ,
,
∴B点坐标为(![]() ,
,![]() ),
),
∵点A到![]() 轴的距离是点B到
轴的距离是点B到![]() 轴距离的2倍,
轴距离的2倍,
∴![]() ,
,
当![]() ,解得
,解得![]() ,此时B点坐标为(
,此时B点坐标为(![]() ,
,![]() );
);
当![]() ,解得
,解得![]() ,此时B点坐标为(
,此时B点坐标为(![]() ,
,![]() );
);
综上所述,B点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)∵点A的坐标为(![]() ,
,![]() ),点B坐标为(
),点B坐标为(![]() ,
,![]() ),
),
∴AB与![]() 轴平行,
轴平行,
∵点D的坐标为(2,![]() ),且
),且![]() ,
,
∴点A、点B在![]() 轴的下方,即
轴的下方,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() ,解得
,解得![]() ,此时B点坐标为(
,此时B点坐标为(![]() ,
,![]() );
);
当![]() ,解得
,解得![]() ,此时B点坐标为(
,此时B点坐标为(![]() ,
,![]() );
);
综上所述,B点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)【特例探究】
如图1,当tan∠PAB=1,c=4 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)【拓展证明】
如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ,AB=3,求AF的长.
,AB=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某电脑公司有A型、B型、C型三种型号的电脑,其价格分别为A型每台6 000元,B型每台4 000元,C型每台2 500元,我市东坡中学计划将100 500元钱全部用于该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该校选择,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
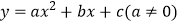 的图象如图,给出下列四个结论:①
的图象如图,给出下列四个结论:① 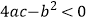 ;②
;② 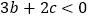 ;③
;③ 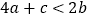 ;④
;④ 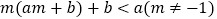 ,其中正确结论的个数是( )
,其中正确结论的个数是( )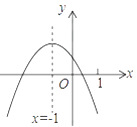
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠ACB=90,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点按顺时针方向旋转90后得CE,连接EF.
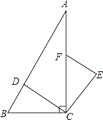
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周六上午,小亮去图书馆查资料,图书馆离家不远,他步行去图书馆,查完资料后他又边走边转去书店买书,在书店停留了几分钟后骑共享单车回家."已知小亮离家的距离
 (米)与离开家的时间
(米)与离开家的时间 (分)之间的关系如图所示.请根据图象回答下列问题:
(分)之间的关系如图所示.请根据图象回答下列问题:(1)小亮出发几分钟后到达图书馆?
(2)小亮查完资料后步行的速度是多少?
(3)小亮
 离开图书馆,几点回到家?
离开图书馆,几点回到家?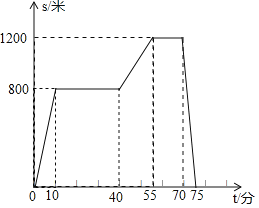
相关试题

