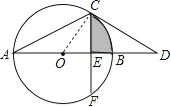
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

参考答案:
【答案】(1) 30°;(2)![]() -2
-2![]() .
.
【解析】试题分析:(1)连接OC,则△OCD是直角三角形,可求出∠COD的度数;由于∠A与∠COD是同弧所对的圆周角与圆心角.根据圆周角定理即可求得∠A的度数;
(2)由图可知:阴影部分的面积是扇形OCB和Rt△OEC的面积差;那么解决问题的关键是求出半径和OE的长;在Rt△OCE中,∠OCE=∠D=30°,已知了CE的长,通过解直角三角形,即可求出OC、OE的长,由此得解.
试题解析:(1)连接OC,
∵CD切⊙O于点C
∴∠OCD=90°
∵∠D=30°
∴∠COD=60°
∵OA=OC
∴∠A=∠ACO=30°;
(2)∵CF⊥直径AB,CF=4![]()
∴CE=2![]()
∴在Rt△OCE中,tan∠COE=![]() ,
,
OE=![]() =2,
=2,
∴OC=2OE=4
∴S扇形BOC=![]() ,S△EOC=
,S△EOC=![]() ×2×2
×2×2![]() =2
=2![]()
∴S阴影=S扇形BOC-S△EOC=![]() -2
-2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,属于必然事件的是
A. 任意投掷一枚硬币,落地后正面朝上;
B. 2019年春节当天北京将下雪;
C. 弟弟的年龄比哥哥的年龄小;
D. 明天早晨,大家能看到太阳从西方冉冉升起.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如3=22-12,16=52-32,则3和16是智慧数).已知按从小到大的顺序构成如下数列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,…则第2 013个“智慧数”是______.
【答案】2 687
【解析】解析:观察数的变化规律,可知全部“智慧数”从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数,归纳可得,第n组的第一个数为4n(n≥2).因为2 013÷3=671,所以第2 013个“智慧数”是第671组中的第3个数,即为4×671+3=2 687.
点睛:找规律题需要记忆常见数列
1,2,3,4……n
1,3,5,7……2n-1
2,4,6,8……2n
2,4,8,16,32……
1,4,9,16,25……

2,6,12,20……n(n+1)
一般题目中的数列是利用常见数列变形而来,其中后一项比前一项多一个常数,是等差数列,列举找规律.后一项是前一项的固定倍数,则是等比数列,列举找规律.
【题型】填空题
【结束】
19【题目】如图,郑某把一块边长为a m的正方形的土地租给李某种植,他对李某说:“我把你这块地的一边减少5 m,另一边增加5 m,继续租给你,你也没有吃亏,你看如何”.李某一听,觉得自己好像没有吃亏,就答应了.同学们,你们觉得李某有没有吃亏?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列代数式能作为二次根式被开方数的是( )
A. 3﹣π B. a C. a2+1 D. 2x+4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,郑某把一块边长为a m的正方形的土地租给李某种植,他对李某说:“我把你这块地的一边减少5 m,另一边增加5 m,继续租给你,你也没有吃亏,你看如何”.李某一听,觉得自己好像没有吃亏,就答应了.同学们,你们觉得李某有没有吃亏?请说明理由.

【答案】李某吃亏了,理由见解析.
【解析】试题分析:计算阴影部分面积和原正方形面积作比较.
试题解析:
解:李某吃亏了.理由如下:
∵(a+5)(a-5)=a2-25<a2,
∴李某少种了25 m2地,李某吃亏了.
【题型】解答题
【结束】
20【题目】计算:(1)992-102×98;
(2)[x(x2y2-xy)-y(x2-x3y)]÷x2y.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《深圳都市报》报道,截止到2017年3月底,深圳共享单车注册用户量超千万人,互联网自行车日均使用量2590000人次,将2590000用科学记数法表示应为
A.0. 259×107
B.2.59×106
C.29.5×105
D.259×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】某地原有沙漠108公顷,绿洲54公顷,为改善生态环境,防止沙化现象,当地政府实施了沙漠变绿洲”工程,要把部分沙漠改造为绿洲,使绿洲面积占沙漠面积的80%.设把x公顷沙漠改造为绿洲,则可列方程为( )
A.54+x=80%×108
B.54+x=80%(108-x)
C.54-x=80%(108+x)
D.108-x=80%(54+x)
相关试题

