【题目】点A(﹣3,y1),B(0,y2),C(3,y3)是二次函数y=﹣(x+2)2+m图象上的三点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3B.y1=y3<y2C.y3<y2<y1D.y1<y3<y2
参考答案:
【答案】C
【解析】
先确定抛物线的对称轴,然后比较三个点到对称轴的距离,再利用二次函数的性质判断对应的函数值的大小.
二次函数y=﹣(x+2)2+m图象的对称轴为直线x=﹣2,
又a=-1, 二次函数开口向下,
∴x<-2时,y随x增大而增大,x>-2时,y随x增大而减小,
而点A(﹣3,y1)到直线x=﹣2的距离最小,点C(3,y3)到直线x=﹣2的距离最大,
所以y3<y2<y1.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形具有而一般平行四边形不一定具有的性质是( )
A. 对角线相等 B. 对角相等 C. 对角线互相平分 D. 对边相等
-
科目: 来源: 题型:
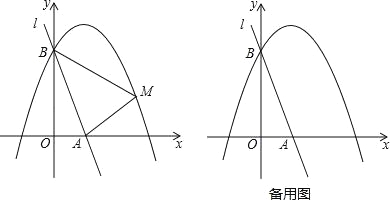
查看答案和解析>>【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.(x2)3=x5B.x2+2x3=3x5C.(﹣ab)3=a3bD.x3x3=x6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣(x+4)2+6的顶点坐标是( )
A.(4,6)B.(﹣4,6)C.(4,﹣6)D.(﹣4,﹣6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(a,3)与点B(﹣4,b)关于原点对称,则a+b=
相关试题

